3^100-2^100=
3^100=1000000
1000000-2=999998
999998^100=999800019798706462737190875649304679855127015839566029857116283692835412472042116519016907412887633139457448348038540437212888477510800359797979480682316195273658223309436710165254896464991999084421212526354729627935676792123224557558171757687033784411273628709459888504432022053487329592260623553564034369148358922766281288488343561474912897905314650643908574171222256789943965310113064773420518280547095879507784945871912713530535276654732698245598090303118206340056616917891563946719274297498872061862362483232594945821769715212505773035207576194541751920170411695449308652637970047041227903205376
последняя цифра-6
![2x+1=y^3\\y= \sqrt[3]{2x+1}](/tpl/images/0179/7261/4c476.png)
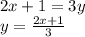
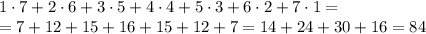
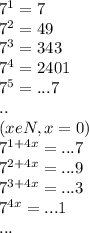
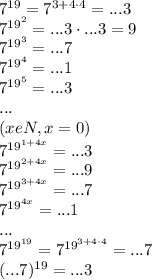
ответ:366