Итак, цена баранины за 1 кг - 250 р., цена телятины на 1 кг - 290 р. Пусть кол-во баранины = х кг, а кол-во телятины = у. Тогда, если баранины на 12 кг больше, чем телятины, то будет справедливо выражение: х-12=у Также нам известно, что масса баранины относится к массе телятины как 18:17, т.е.: х = 18 у 17
Получаем систему уравнений: х-12=у
х = 18 у 17
Из первого уравнения у подставим во второе: х = 18 х-12 17
Решим его относительно х: 17х=18(х-12) 17х=18х-18*12 17х=18х-216 216=18х-17х х=216 кг - масса проданной баранины. Тогда масса проданной телятины будет: х-12=у=216-12=204 кг
Нужно найти стоимость проданного мяса. Её мы найдём, как сумму денег, которую выручили за баранину и за телятину. Напомню, что, цена баранины за 1 кг - 250 р., цена телятины на 1 кг - 290 р. Масса проданной баранины 216 кг, масса проданной телятины 204 кг. 250*216+290*204=54000+59160=113160 р. - стоимость всего мяса.
Стоит заметить, что если мы умножим первое уравнение системы на 2, то получим одинаковые коэффициенты при х, а именно : 4. Так умножим же первое уравнение на 2 (хочу заметить, что решение уравнения никак не изменится после таких манипуляций). При умножении уравнения на 2, нужно каждое слагаемое умножить на 2: 4х-6у=12 -4х+6у=-12
Теперь складываем уравнения. Сложение уравнений происходит таким образом: каждое подобное слагаемое складывается с себе подобным (х с х, у с у, свободные числа с числами), т.е.: 4х+(-4х)-6х+6х=12+(-12) 4х-4х+0=12-12 0+0=0 0=0
На самом деле можно было получить то же самое, если второе уравнение разделить на 2 и так же сложить с первым.
На самом деле поучается, что первое уравнение системы-это второе, только умноженное на -1. Поэтому от системы остаётся оно уравнение: 2х-3у=6 Выразим из него у, получив функцию: 3у=2х-6 у=2x/3 - 2 При задании некоторых значений х, будем получать соответствующие этим значения значения у. ответ: у=2х/3 - 2.
27
35
Пошаговое объяснение:
1) х =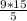 = 27
= 27
2) х =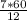 = 35
= 35