
Возьмем первый член прогрессии за y, 2-ой - за z. Итак, дана прогрессия: y, z, y-6, z+3, ... Знаменатель прогрессии обозначим как х, т.е. каждое последующее число больше предшествующего в х раз. Тогда: z=xy; y-6=x^2*y; z+3=xy-6x; В заключительном случае z заменим на xy: ху+3=ху-6х; ху-ху+3=-6х; -6х=3; х=3/(-6)=-0,5; Итак, знаменатель прогрессии равен -0,5. Тогда: z/у=-0,5; (у-6)/z=-0,5; (z+3)/y-6=-0,5. Решим уравнение: (у-6)/z=-0,5; Заменим z на -0,5у: (у-6)/(-0,5у)=-0,5; у-6=-0,5*-0,5у; у-6=0,25у; у-0,25у=6; 0,75у=6; у=6/0,75=8 - 1-ый член; z=-0,5*8=-4 - 2-ой член; у-6=8-6=2 - 3-ий член; z+3=-4+3=-1 - 4-ый член. ответ: 8; -4; 2; -1.
Пошаговое объяснение:
Обозначим четыре части: a; b; c; d.
По условию:
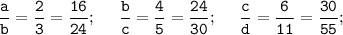
Очевидно, что а = 16; b = 24; c = 30; d = 55
a + b + c + d = 16 + 24 + 30 + 55 = 125
Первая дробь: числитель и знаменатель умножаем на 8, вторая - на 6, третья - на 5. Такой выбор множителей нужен для того, чтобы уравнять значение b, в первом и втором соотношении, и значение с - во втором и третьем соотношении.
Сумма частей, полученная при этом, не обязательно будет равняться исходному числу, но, в любом случае, она будет ему кратной.
Например, исходное число при тех же соотношениях между частями, равно 375. Так как мы в сумме получили 125 "микрочастей", то каждая такая часть, в этом случае, равняется 3, и число 375 разбивается на:
16*3 + 24*3 + 30*3 + 55*3 = 48 + 72 + 90 + 165 = 375.
=========================
Для тех, кто, все-таки, решает эту задачу уравнением..))
Воспользуемся основным свойством пропорции:
3a = 2b; 5b = 4c; 11c = 6d
Сложим левые и правые части:
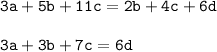
Постараемся в левой части оставить выражение, кратное a+b+c+d, которое, по условию, равно 125:

ответ: 16; 24: 30; 55.
осылайау деп ойлаймын