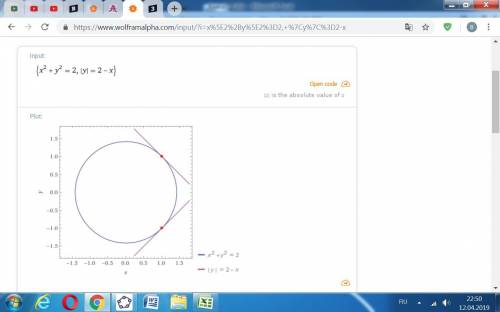
Заданная система уравнений х^2 + у^2 = 2, х+|y| = a графически представляет собой 3 фигуры:
- окружность х^2 + у^2 = 2,
- прямую у = -х + а,
- прямую у = х - а.
Эти прямые взаимно перпендикулярны и чтобы было 2 решения, они должны касаться окружности каждая в одной точке.
Радиусы в точку касания параллельны прямым, но так как они идут из начала координат, то их уравнения у = х и у = -х.
Возьмём у = х и у = -х + а и приравняем: 2х = а, х =а/2, но и у = х = а/2.
Подставим ув уравнение окружности: (а²/4) + (а²/4) = 2, 2а² = 8,
а² = 8/2 = 4. Отсюда а = +-2.
ответ: наибольшее значение параметра а равно 2.
Пошаговое объяснение:
2х+2у=1
2у=1-2х
6y=3(1-2x)
6y=3-6x
Подставляем.
2x²-3-6x=5
Получаем кв. уравнение.
2x²-6x-8=0
D=b²-4ac=36+64=100
x1=6-√100/2*2=6-10/4=-4/4=-1
x2=6+√100/2·2=6+10/4=16/4=4
ответ: -1; 4.
Сделай лучшим