Пошаговое объяснение:
Введем замену 
; 
.
Уравнение примет вид
Далее заметим, что для любого 
верно 
. То есть верхнее ограничение 
выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения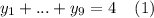 
в целых неотрицательных числах.
А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].
Искомое количество вариантов
23 шарика
Пошаговое объяснение:
Пусть имеется некоторое количество n шариков.
Тогда n - такое число, которое:
1. при делении его на 8 даёт остаток 7
2. при делении его на 6 даёт остаток 5
3. при делении его на 4 даёт остаток 3
4) n < 45
Из первых трёх пунктов следует, что число n + 1 делится на 8, 6 и 4. Найдём НОК (8,6,4), которое делится на 8, 6, 4 без остатка и которое меньше 45:
НОК чисел 8,6,4 - 24
24 - 1 = 23 < 45
24 * 2 - 1 = 47 > 45
Следовательно, шариков было 23.
Проверим:
23 : 8 = 2 (ост.7)
23 : 6 = 3 (ост.5)
23 : 4 = 5 (ост.3)