Наш посёлок самый хороший мы не балуемся со огнём и не уничтожаем деревьев но есть люди кто незнает как обращяться с природой кто то разжигает траву сохшую приводит к пожару ещё выбрасывают мусор и различные химикаты которые поподают в почву разжигают костры туда бросают бутылки потом начинаеться подниматься едкий дым которые деревья или растения погибают . Ещё отбрасывают атходы может привести болезни .Надо беречь свой посёлок и ненадо так делать лутше всего закопать в землю и всё а потом дела бактерий.
y=kx+b -прямая. Расположение зависит от коэффициента при x(сейчас это k). Если k положительный, то график проходит в 1 и 3 плоскостях, а если нет- во 2 и 4. Строится табличным парабола. Число при x так же отвечает за вид графика. Если a положительное, то ветви параболы направленны вверх, а если отрыцательное- вниз. Чтобы построить параболу нужно сначала найдем ее x вершину: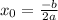 
, затем эту X вершину подставляем в 
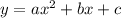и находим Y вершину. Далее нужно найти точки пересечения осей графика. Для этого обозначаем X и, затем, Y за 0 и находим точки пересечения осей. Параболу можно строить и табличным Если при X степень нечетная( не квадрат, а куб, нарпимер), тогда парабола имеет другой вид: одна ее ветка направлена вверх, другая- вниз.
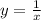-гипербола (X- обязательно знаменатель!). Находится или в 1 и 3 плоскосли, или во 2 и 4. В этой функции X не может быть 0, поэтому гипербола никогда не пересечет ни ось абцисс, ни ось ординат. Строится табличным одна ветка параболы. X не может быть отрицательным. Строится табличным прямые. Имеет форму галочки. Одна прямая симетрична другой. X может быть как больше 0, так и меньше 0. Направление веток определяет коэффициент при модуле(-|X| или |X|).
за 1 3/7 часа наполнится бассейн, если включить оба насоса
Пошаговое объяснение:
Наполненный бассейн примем за единицу (одна целая часть).
1) 1 : 3 1/3 = 1 : 10/3 = 1 * 3/10 = 3/10 части бассейна, наполняемая первым насосом за 1 час;
2) 1 : 2 1/2 = 1 : 5/2 = 1 * 2/5 = 2/5 части бассейна, наполняемая вторым насосом за 1 час;
3) 3/10 + 2/5 = 3/10 + 4/10 = 7/10 части бассейна, наполняемая через оба насоса за 1 час;
4) 1 : 7/10 = 1 *10/7 = 10/7 = 1 3/7 (часа) - время наполнения бассейна, если включить оба насоса сразу.