1) Слово «абсцисса» заимствовано из французского языка в начале XIX века. В свою очередь, фр. abscisse происходит от лат. abscissa, возникшего в результате субстантивации прилагательного после эллипсиса существительного linea (из лат. abscissa linea — "отрезанная, оторванная линия")
Слово «ордината» происходит от лат. ordinatus — «расположенный в порядке». Впервые термин «ордината» применил немецкий учёный Г. Лейбниц в 1694 году. Древнегреческий математик Аполлоний Пергский называл параллельные хорды «по порядку проведенными линиями» (от лат. ordinatum apllicatae — «по порядку приложенная»)
2)Наречие «перпендикулярно» происходит от существительного «перпендикуляр». Это слово пришло в русский язык из латыни. Там per и pendere означало «перед» и «висеть», а сочетание этих двух слов можно перевести как «отвес». Словосочетание показалось очень удобным, и его стали применять в геометрии.Перпендикуляром можно назвать прямую. Но не каждую, а лишь ту, которая находится под прямым углом. Поэтому ответ на вопрос о том, что значит перпендикулярно, обязательно должен содержать упоминание прямого угла. Прямая может быть перпендикулярна другой прямой, лучу, вектору, стороне геометрической фигуры и даже плоскости.
3) В евклидовой геометрии параллельными прямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются.
4) Происходит от прил. параллельный, из др.-греч. «идущий вдоль другого», далее из παρά «возле, рядом» «взаимно, друг друга» (другой, иной»). В ряде европейских языков слово заимств. через лат. parallelus.
Русск. параллель — впервые у Петра I. Заимств. через франц. parallèle или нем. Раrаllеl ж. из лат.
Правильная четырехугольная пирамида 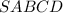 .
.
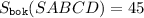 (см²).
(см²).
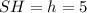 (см).
(см).
 - сторону основания.
- сторону основания.
Площадь боковой поверхности правильной четырехугольной пирамиды можно вычислить по следующей формуле:
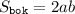 , где
, где  - сторона основания и
- сторона основания и 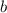 - апофема (высота боковой грани, проведенная из вершины).
- апофема (высота боковой грани, проведенная из вершины).
Попробуем выразить 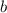 через
через  (сторону основания) и
(сторону основания) и 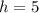 (см) (высоту пирамиды).
(см) (высоту пирамиды).
Рассмотрим прямоугольный 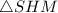 (где
(где 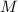 - середина
- середина 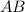 ). В нем
). В нем 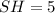 (см), а
(см), а 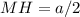 (см) (как половина стороны квадрата, равной
(см) (как половина стороны квадрата, равной  см).
см).
По теореме Пифагора:
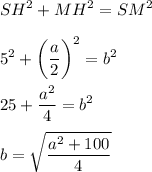
Все это подставляем в уравнение площади боковой поверхности (при возведении в квадрат держим в голове, что  - неотрицательное):
- неотрицательное):
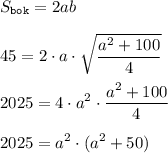
Пусть 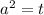 :
:
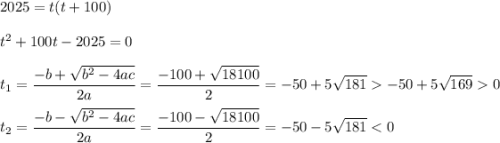
Второй корень нам не подходит по причине отрицательности. Значит:
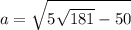
Задача решена!
ответ: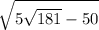 или около
или около 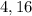 (см).
(см). 
( x, y)=(4, -3)
Пошаговое объяснение: