
Чтобы найти НОД чисел нужно разложить их на простые множители и перемножить между собой общие множители (подчёркнуты).
Чтобы сократить дробь, нужно числитель и знаменатель разделить на НОД.
1) 24 = 2 * 2 * 2 * 3
60 = 2 * 2 * 3 * 5
НОД (24; 60) = 2 * 2 * 3 = 12

2) 45 = 3 * 3 * 5
105 = 3 * 5 * 7
НОД (45; 105) = 3 * 5 = 15
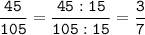
3) 39 = 3 * 13
130 = 2 * 5 * 13
НОД (39; 130) = 13
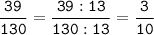
4) 64 = 2 * 2 * 2 * 2 * 2 * 2
144 = 2 * 2 * 2 * 2 * 3 * 3
НОД (64; 144) = 2 * 2 * 2 * 2 = 16
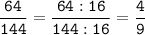
===========================================================
Чтобы найти НОК чисел, нужно разложить их на простые множители и к множителям бОльшего числа добавить недостающие множители (подчёркнуты) и перемножить их между собой.
Наименьшее общее кратное и будет наименьшим общим знаменателем.
1) 12 = 2 * 2 * 3
8 = 2 * 2 * 2
НОК (12; 8) = 2 * 2 * 3 * 2 = 24


2) 9 = 3 * 3
15 = 3 * 5
НОК (9; 15) = 3 * 5 * 3 = 45

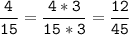
3) 25 = 5 * 5
15 = 3 * 5
НОК (25; 15) = 5 * 5 * 3 = 75
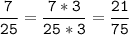
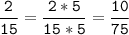
4) 16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
НОК (16; 24) = 2 * 2 * 2 * 3 * 2 = 48
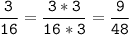
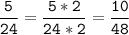
Когда кость бросается дважды, возможно 6*6=36 исходов - оба раза может выпасть любое число от 1 до 6. Обратите внимание, что нам важно, какое число выпало первым, а какое вторым - например, (2,1) и (1,2) - это два разных исхода. Для события А существует 3 благоприятных исхода - (5,6), (6,5), (6,6). Тогда P(A)=3/36=1/12. Для события Б существует 36/2=18 благоприятных исходов - (1,1), (1,3), (1,5), (2,2), (2,4), (2,6), ..., (6,2), (6,4), (6,6). Таким образом, вероятность события Б равна 18/36=1/2.