Пошаговое объяснение:
Для соответствия Г=(X, Y, G) определить набор свойств, которыми обладает данное соответствие: X = R, Y - функции, непрерывные на [0, 1], G = (m, f(x)|minf(x) = m). То есть соответствие состоит из пар (число, функция), причём пара есть не для любого числа и функции, а только если это число является минимумом функции.
Я думаю так:
1) всюду определённость не выполняется (так как не любое число является минимумом функции);
2) сюръективность не выполняется (так как не для каждой функции можно найти минимум);
3) функциональность не выполняется (так как одно число может быть минимумом более чем для одной функции);
4) инъективность выполняется (так как функция имеет только один минимум).
1)Х=-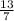
2)Х=-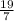
Пошаговое объяснение:
1)-5(x+3)-6=2(x-4)
-5x-15-6=2x-8
-5x-2x=-8+21
-7x=13
x=-7/13
2)-4(x+8)-2=-3(5-x)
-4x-32-2=-15+3x
-4x-3x=-15+34
-7x=19
x=-19/7