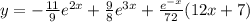
Пошаговое объяснение:
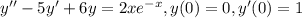
Имеем дело с неоднородным линейным уравнением. Его решение можно искать в виде суммы общего решения однородного уравнения и частного решения неоднородного: 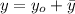
Однородное уравнение: 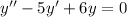
Его характеристическое уравнение: 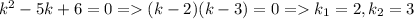
Общее решение однородного уравнения запишется в виде:
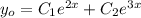
Частное решение неоднородного уравнения имеет смысл искать в виде: 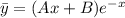
Посчитаем производные:
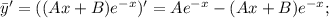
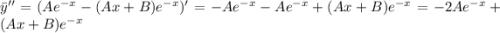
Подставляем в уравнение и сокращаем на экспоненту:
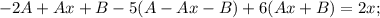
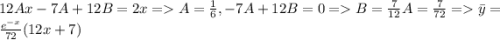
Тогда общее решение запишется в виде:
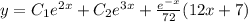
Определим константы из начальных условий:
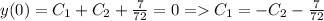
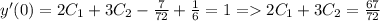
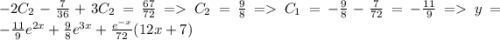
(1600; -⁶√1,25); (1600; ⁶√1,25)
Пошаговое объяснение:
пусть y⁶ = t ≥ 0
{xt² = x + 900
{xt² - 400t = 2000
отнимем от первого второе:
400t = x - 1100
x = 400t + 1100
подставим во второе:
400t³ + 1100t² - 400t = 2000
4t³ + 11t² - 4t - 20 = 0
проверим t = -2
-32 + 44 + 8 - 20 = 0; t = -2 - корень
4t³ + 11t² - 4t - 20 = 4t²(t + 2) + 3t² - 4t - 20 = 4t²(t + 2) + 3t(t + 2) - 10(t + 2) =
=(t + 2)(4t² + 3t - 10) = 0
D = 9 + 160 = 13
t2 = (-3 - 13)/8 = -2
t3 = (-3 + 13)/8 = 5/4 = 1,25
y⁶ = 1,25 => x = 400 * 1,25 + 1100 = 1600
y1 = -⁶√1,25
y2 = ⁶√1,25