х (км/ч) - скорость течения реки
(20 - х) км/ч - скорость катера против течения
(20 + х) км/ч - скорость катера по течению
Тогда время, затраченное на путь против течения равен:
36/(20 - x) ч
А время пути по течению реки:
22/(20 + x) ч
Составим уравнение:
36/(20 - x) + 22/(20 + x) = 3
36/(20 - x) + 22/(20 + x) - 3 = 0 x ≠ 20, x ≠ - 20
720 + 36x + 440 - 22x - 3 * (20² - x²) = 0
1 160 + 14x - 1 200 + 3x² = 0
3x² + 14x - 40 = 0
D = 14² - 4 * 3 * (- 40) = 196 - (- 480) = 676
= 
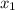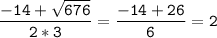км/ч
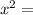
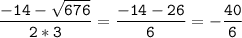- не подходит под условие
ответ: скорость течения реки равна 2 км/ч.
у1 - мощность первого насоса, у2 - второго.
Составим уравнение (1) :
два насоса накачают за 6 часов : (у1 + у2) * 6 = х ( 1 )
Уравнеие (2) : Один насос за 15 часов. : 15 * у1 = х ( 2 )
РЕШЕНИЕ
(у1+у2)*6=х 6у1+6у2=х 6у2=х - 6у1 у2= ( х - 6у1 ) /6 Подставляем в полученное уравнение вместо ( х ), его значение из ( 2 )
тогда у2=(15у1-6у1)/6
у2 =9у1/6
у2=1,5у1
Из этого следует, что мощность второго в полтора раза больше первого, тогда и накачает второй насос в полтора раза быстрее первого.
Значит : 15 / 1,5 = 10 часов надо второму... .