3) при х = 1
Пошаговое объяснение:
При каком-то х произведение 2*x должно являться простым числом, то есть делится только на 2x и на 1. А 2x делится и на 2х, и на х, и на 1
Тогда нужно, чтобы совпали какие-то 2 делителя. Имеем 3 варианта:
1) 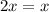 , откуда
, откуда 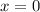 , но тогда 2х равно 0 - не простое.
, но тогда 2х равно 0 - не простое.
2) 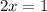 , откуда
, откуда 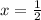 , но тогда 2х равно 1 - не простое
, но тогда 2х равно 1 - не простое
3) 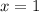 , откуда 2х = 2 - простое
, откуда 2х = 2 - простое
На какое максимальное количество кусочков можно нарезать арбуз за 10 разрезов?
Предположим, у нас есть всё необходимое оборудование для выполнения следующих действий:
В начале у нас целый арбуз ( 1 ). Первый разрез - поделили его на 2 кусочка. Далее, внимательно (важно уловить ход мысли и поймете всё решение), можно сложить эти 2 кусочка в 1 ряд, чтобы прибором сделать разрез сразу 2 кусочков, отчего получим 4. Далее четыре складываем таким же образом и получаем 8.
Таким образом максимальное количество кусочков равно:
1 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 = 1024
ответ: 1024 кусочка
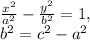
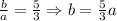
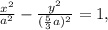
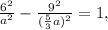
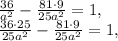
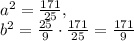
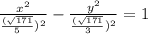
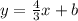
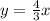
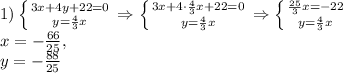
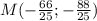
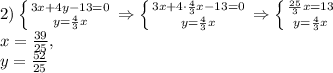
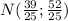
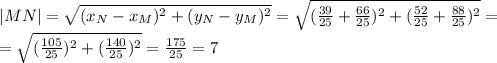
ответ:3) 1
Пошаговое объяснение: