Какие высказывания являются верными, а какие - неверными? (верныевысказывания o'zmeі» те знаком «+», неверные - знаком 4 р.)1) если диагонали четырёхугольника равны и перпендикулярны,то этот четырехугольник - квадрат2) если в четырехугольнике две пары равных углов, то этот четы-рёхугольник - параллелограмм3) если диагонали четырехугольника перпендикулярны, то тотчетырехугольник - прямоугольник
 . Есть константа(число) и переменные, содержащие степень. А например
. Есть константа(число) и переменные, содержащие степень. А например 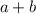 одночленом уже не будет.
одночленом уже не будет.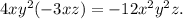 .
. 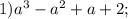
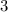

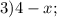
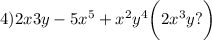
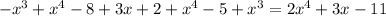
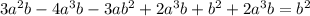
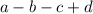 в виде:
в виде: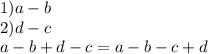
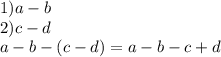
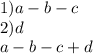

 и
и 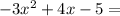 .
.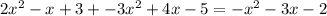
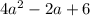 и
и 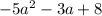 .
.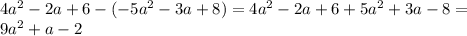
 и
и 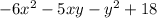 .
.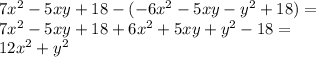
Треугольник – это геометрическая фигура, которую образуют три отрезка, соединяющие три точки, не расположенные на одной прямой.
Значит, чтобы узнать периметр треугольника, надо знать длины всех его сторон. Если треугольник равнобедренный, достаточно знать длины двух сторон. Соответственно, если равносторонний – надо знать длину только одной стороны.
Периметр получим, сложив все три длины вместе: P = a + b + c.
Задачи про периметр треугольника:
Найдите периметр равностороннего треугольника со стороной 5 см.Так как все стороны треугольника равны, просто умножим длину стороны на 3 и получим нужное нам значение периметра: Р = 5*3 = 15 см.Задача для подготовки к ГИА: Известно, что периметр равнобедренного треугольника – 90 см, его боковая сторона имеет длину 25 см. Требуется найти длину основания треугольника.
Раз треугольник равнобедренный, его боковые стороны равны. Зная это, можем составить простое уравнение: 90 = 50 + с, откуда получаем с = 90 – 50 = 40. Это и есть искомая длина основания.Как находить периметр четырехугольника
К четырехугольникам относятся прямоугольник, квадрат, ромб, параллелограмм, трапеция.
Периметр прямоугольника
Прямоугольник – это параллелограмм со всеми прямыми углами.
Стороны этой геометрической фигуры попарно равны. Поэтому чтобы определить периметр, достаточно сложить его ширину и высоту, а затем умножить полученное число на два. P = 2*(a + b).
Задачи про периметр прямоугольника:
Имеется бассейн прямоугольной формы. Его периметр составляет 80 м, а ширина – 15 м. Найдите, какова длина этого бассейна.Помня, что периметр складывается из удвоенной суммы длины и ширины, запишем известные и неизвестные нам величины в виде уравнения: 80 = 2*(15 + b). А потом раскроем скобки и соберем все известные нам величины по одну сторону знака равенства, а все неизвестные – по другую: 80 – 30 = 2b. Из чего уже легко вычислить, какова же длина бассейна: b = (80 – 30)/2 = 25 м.Задача для подготовки к ГИА. Дан периметр прямоугольника, равный 42 см. Также известно, что отношение длины и ширины составляет 4:3. Требуется вычислить площадь этого прямоугольника.
Используя известное нам из условий задачи отношение сторон, обозначим длину прямоугольника как 4у, а ширину – как 3у. Помня формулу определения периметра прямоугольника, запишем такое уравнение: 4у + 4у + 3у + 3у = 42. упростим его до 14у = 42. И найдем у: у = 42/14, у = 3. Теперь найдем длину прямоугольника – 4*3 = 12 и ширину – 3*3 = 9. Формула площади прямоугольника: S = a*b. Искомая площадь прямоугольника S = 12*9 = 108 см2.
Периметр квадрата
Квадрат – тот же прямоугольник, только все его стороны равны друг другу, все углы прямые.
Определить периметр квадрата можно двумя простым и посложнее.
Простой Т.к. все стороны квадрата равны, надо умножить длину стороны на 4: P = 4*a.
Более сложный Определение периметра квадрата через длину его диагонали. Для этого нужно длину диагонали умножить на два корня из двух: P = d*2√2.
Задачи по периметр квадрата:
Периметр квадратной клумбы с пионами – 24 м. Найдите сторону этой клумбы.Помним, что периметр квадрата – это умноженная на 4 длина его стороны. Поэтому запишем такое равенство: 4*а = 24. Откуда получим а = 24/4 = 6. Длина стороны клумбы составляет 6 м.Задача для подготовки к ГИА. Дан периметр квадрата – 40 см. Надо вычислить его площадь.
Сторону квадрата найдем исходя из формулы периметра: 4а = 40, откуда а = 40/4 = 10 см. Формула площади квадрата: S = a2. Искомая площадь квадрата S = 102 = 100 см2.г