1.
1)Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую. 2)Ставим в частном запятую, когда заканчивается деление целой части делимого Например: 310,1:100 = 3,101 27,56:10= 2,756 0,75:100 = 0,0075 2,2:2=1,1 35,5:5=7,1 Сначала делим как обычно числа мы делили Потом смотрим, и где нужно ставить запятые.
2.
Пусть a делимое и b делитель. По условию делимое меньше делителя: a < b. Число можно представить в виде:
a=k·b+o, где k - частное (целая часть отношения a/b, то есть k=[a/b]), o - остаток от деления и |o|<b, |*| - модуль числа.
По определению: целая часть числа - эта наибольшее целое число, не большее самого числа.
Тогда
1) если 0<a<b или a<b<0, то частное k=0, например:
5 = 0·7+5 или -5 = 0·(-7)-5;
2) если a<0<b, то частное k=[|a/b|]-1, например:
-5 = -1·7+2 или -10 = -2·7+4
Пошаговое объяснение:
Надеюсь (
Если все числа правильно записаны, то ответ получается вот такой ( смотри ниже. Но смущают не целые числа, хотя всё остальное правильно)
Пошаговое объяснение:
Пусть во 2 день продали на х сум, тогда по условию в 1 день ( х + 23500) сум, а в 3 день ( х + 23500 - 56000) = ( х - 32500). Всего продано на
1 971 500 сум. Составим и решим уравнение:
( х + 23500) + х + ( х - 32500) = 1 971 500
3х - 9000 = 1 971 500
3х = 1 971 500 + 9000
3х = 1 980 500
х= 1 980 500 : 3
х = 660 166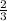
Значит, во второй день было продано на 660 166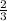 сум, тогда в первый день на 683 666 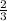сум, а в трети1 день 627 666 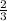сум.
38
Пошаговое объяснение:
Пускай нам дана равнобедренная трапеция ABCD
отрезки, на которые диагональ разбивает среднюю линию, являются средними линиями ∆ ABD и ∆ DBC
АВ = 4*2 = 8
DC = 5*2 = 10 (основание треугольника в два раза больше средней линии)
диагональ DB делит <ABC на два равных угла <ABD = <DBC
<ABD = <BDC (накрест лежащие) ==>
<DBC = <BDC и значит ∆DBC - равнобедренный,
DC = BC = 10
BC = AD = 10 см (боковые стороны трапеции)
P abcd = AB+BC+DC+AD= 8+10+10+10=38 см