у 1 - платьев нет, у 2й - 24, а полное счастье - 25
Пошаговое объяснение:
Если допустить что у 1й есть 1 платье, тогда счастье = 26,
тогда у 2й - для счастья не хватает 1, следовательно у нее есть 25 платьев.
но Вместе им также не хватает хороших платьев для «полного счастья»., а у нас выходит: 1+25=26.
Увеличивая наличие платьев у 1й, увеличивается количество для счастья, и соответственно сумма имеющихся платьев становиться больше счастья.
Следовательно у 1й - 0 платье, тогда счастье = 25,
у 2й - для счастья не хватает 1, следовательно у нее есть 24 платья.
Вместе 0+24 = 24, что меньше счастья "25".
Пошаговое объяснение:
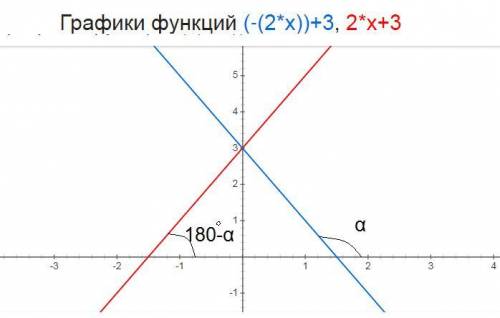
I вариант решения
пусть прямая симметричная прямой y=-2x+3 имеет вид у=kx+b
найдем точки пересечения прямой y=-2x+3 с осями координат относительно оси ОУ
с осью ОХ у=0; -2x+3=0; 2x=3; x=1,5; (1,5;0)
с осью ОY x=0; y=3; (0;3)
так как прямые симметричны то
- они обе проходят через точку (0;3)
- симметричная прямая проходит через точку противоположную точке (1,5;0) точку (-1,5;0)
⇒ симметричная прямая проходит через точки (0;3) и (-1,5;0)
подставим координаты точки (0;3) в уравнение симметричной прямой у=kx+b координату точки (0;3)
получим 3=к*0+b; b=3
подставим координаты точки (-1,5;0) и значение b=3 в уравнение симметричной прямой у=kx+b получим
0=-1,5к+3 ; 1,5к=3; k=3/1,5=2
подставим b=1; k=2 в уравнение у=kx+b
у=2х+3
===============================================
II вариант решения - тригонометрический
так как прямые симметричны то их углы наклона к оси ОХ будут в сумме давать 180°
так как tg(180°-а)=-tga то угловые коэффициенты симметричных прямых будут к₁ и к₂ противоположными числами а значение b₁ и b₂ будут одинаковыми так как обе прямые пересекают ось ОУ в одной точке ⇒ к₂=-к₁=-(-2)=2; b₂=b₁=3
уравнение прямой симметричной прямой y=-2x+3 относительно оси ОУ
у=2х+3
ответ: 13.
Пошаговое объяснение:
21,7-3,1-х=5,6.
21,7-3,1-5,6=х.
х=13.