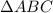 как:
как: ;
; ;
;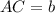 ;
;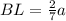 ;
;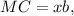 где
где  – некоторое число,
– некоторое число,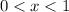 ;
;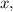 мы найдём и пропорцию, в которой
мы найдём и пропорцию, в которой 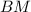 делит сторону
делит сторону 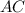 ;
;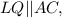 тогда по трём углам:
тогда по трём углам: 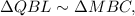
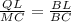 и
и 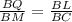 ;
;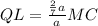 и
и 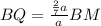 ;
;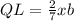 и
и 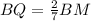 ;
;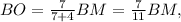 то:
то: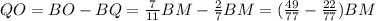 ;
;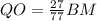 ;
;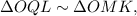 а значит:
а значит: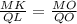 и
и 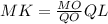 ;
;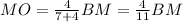 и по [1]
и по [1] 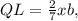 то:
то: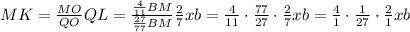 ;
;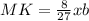 ;
;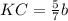 ;
;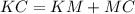 ;
;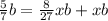 ;
;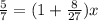 ;
;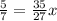 ;
;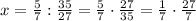 ;
;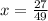 ;
;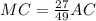 и
и 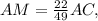 откуда ясно, что отношение, в котором точка
откуда ясно, что отношение, в котором точка 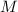 делит сторону
делит сторону 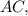 считая от точки
считая от точки 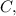 будет:
будет: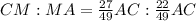 ;
;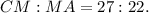
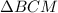 с секущей
с секущей 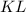 :
: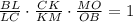 ;
;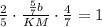 ;
;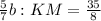 ;
;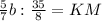 ;
;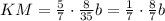 ;
;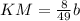 ;
;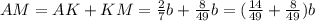 ;
;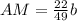 ;
;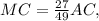 откуда ясно, что отношение, в котором точка
откуда ясно, что отношение, в котором точка 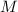 делит сторону
делит сторону 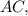 считая от точки
считая от точки 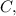 будет:
будет: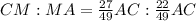 ;
;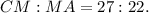
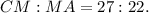
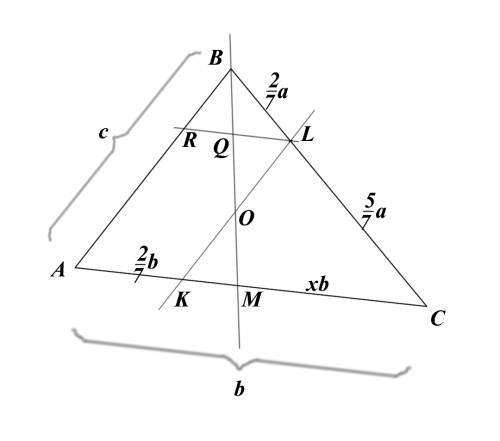
ответ:х=1
Пошаговое объяснение:можно по свойству функций. На графике есть единственная точка пересечения. которую легко угадать. это х=1.
Дело в том. что справа убывающая функция, т.к. это линейная с угловым отрицательным коэффициентом.
а слева возрастающая показательная функция. т.к. основание больше единицы.