
![\displaystyle\begin{cases}\displaystyle\frac{1}{xy}+\frac{1}{x+y}=\frac{1}{2}\\x^2y+xy^2=-2\end{cases}\to\left[\begin{array}{c}x+y=a\\xy=b\end{array}\right] \to\begin{cases}\displaystyle\frac{1}{b}+\frac{1}{a}=\frac{1}{2}\\ab=-2\end{cases}\\\frac{1}{b}+\frac{1}{a}=\frac{1}{2}\\\frac{a+b}{ab}=\frac{1}{2}\\\frac{a+b}{-2}=\frac{1}{2}\\a+b=-1\to a=-(b+1)\\-b(b+1)=-2\\-b^2-b=-2\\b^2+b-2=0\\b_1=1;b_2=-2\\a_1=-2;a_2=1](/tpl/images/3843/9685/b1b03.png)
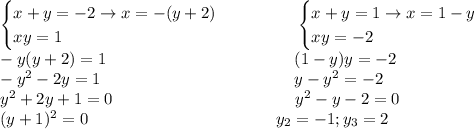

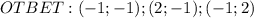
Г. (-1,2), (2,-1)
Пошаговое объяснение:
а=х+у в=ху
Первое уравнение: 1/а+1/в=1/2 или а+в=ав/2
Второе урнение ав=-2
Подставим в первое а+в=-1
По теореме виета а и в корни квадратного уравнения
t^2+t-2=0 a=1 в=-2 (можно и без теоремы Виета , подставить а=-2/в и получить тоже самое). Понятно, что а=-2 в=1 тоже корни.
Теперь найдем х и у
ху=-2 х+у=1 это тоже корни уравнения , теперь уже
t^2-t-2=0 x=-1 y=2 или х=2, у=-1. Это ответ
Відповідь
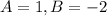
Покрокове пояснення:
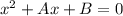 - наше квадратне рівняння
- наше квадратне рівняння
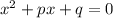 - загальне квадратне рівняння
- загальне квадратне рівняння
Виходить, що 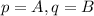
А з умови здачі маємо, що:
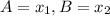 - корені
- корені
Тоді, за теоремою Вієта маємо:
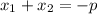 ⇒
⇒ 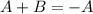 (1)
(1)
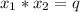 ⇒
⇒ 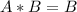 (2)
(2)
З рівняння (2) визначаємо A:
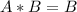 ⇒
⇒ 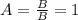 ⇒
⇒ 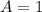
З рівняння (1) визначаємо B:
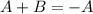 ⇒
⇒  ⇒
⇒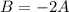 підставляємо в це рівняння значення A=1
підставляємо в це рівняння значення A=1
Виходить  ⇒
⇒ 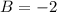
Можна зробити перевірку щоб впевнитись у правильності відповіді, підставляючи A та B в наше рівняння, отримаємо:
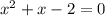 і за дискримінантом розв'язуємо це рівняння
і за дискримінантом розв'язуємо це рівняння
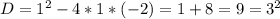
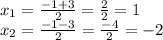
Коефіцієнти правильні, тобто дорівнюють кореням
Пошаговое объяснение:
чтобы найти скорость первого мотоциклиста, мы используем формулу: V=S:t.
далее по этой формуле решаем:
V=270:3=90км/ч. Это скорость первого мотоциклиста.
далее узнаем скорость второго мотоциклиста. к скорости первого мы прибавляем разницу:
90+30=120км/ч. Это скорость второго.
далее мы ищем расстояние. так же по формуле S=Vt:
S=120*3=360км. Расстояние второго мотоциклиста.
вторая задача решается по аналогии.
находим первую скорость автомобиля по формуле. далее ищем вторую скорость. и потом ищем второе расстояние тоже по формуле. весь ответ в картинке
