Угловой коэффициент касательной к графику функции равен производной функции в точке касания.
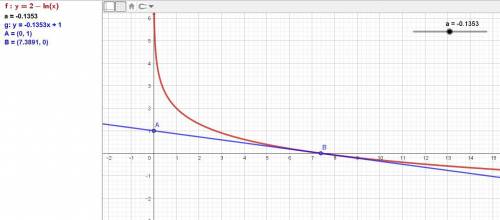
Производная функции y=2-lnx равна -1/x.
Значит, уравнение касательной имеет вид y = (-1/x)*x+ 1 или y = 0.
В точке касания координаты кривой и прямой равны.
Приравняем: 2 - lnx = 0, отсюда x = e².
Точка касания В = (e²; 0).
Известна точка прямой на оси Оу - это свободный член уравнения прямой, то есть у = 1 при х = 0.
По двум точкам находим угловой коэффициент касательной.
k = Δy/Δx = (0 - 1)/(e² - 0) = -1/e².
ответ: а = -1/e².
7
Пошаговое объяснение:
Задание.
Найти кратчайшее расстояние от точки A(6,-8) к окружности (х²+y²= 9).
Решение.
1) Уравнение х²+y²= 9 описывает окружность радиуса R = √9 = 3, с центром в точке О (0;0), т.к. а = 0 и b = 0.
2) Соответственно кратчайшим расстоянием между точкой А (6; -8) и радиусом данной окружности будет разность между длиной отрезка ОА и радиусом данной окружности, равным 3.
3) Находим длину отрезка ОА:
ОА = √(6²+(-8)²=√(36+64)=√100 = 10.
4) Кратчайшее расстояние от точки A(6,-8) к окружности (х²+y²= 9) равно: 10 - 3 = 7.
ответ: 7.
ответ: первая сторонах
2сторона-3х
3строна-4х
4сторона -5х
Уравнение:
Х+4х+5х+3х=240
13х=240
Х=20
5×20=100-наибольшая сторона
Пошаговое объяснение: