1) При равенство примет вид , следовательно, при имеем верное равенство.
2) Предположим справедливость этого утверждения для , где — произвольное натуральное число, и с учетом этого предположения установим справедливость для
Следовательно, при имеем истинное утверждение.
3) Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального .
сегодня то есть 18 апреля у меня день рождения я его уже отпраздновал Он был очень веселый я познал много своих друзей Катю Ваню Машу Лизу Сначала мы пошли в кино она в первом мстителе Противостояние Мне очень понравилось фильм он был очень интересный потом мы поехали ко мне домой родители заказали большой торт Мы ели картошку фри курицу в кляре и пельмени Зачем Мы поели торт и поиграли в разные подвижные игры на тему мои друзья ушли но они мне подарили очень много разных подарков на этом и закончился мой день рождения
Справочник - Природоведение Когда солнце нагревает поверхность рек, озёр и морей, часть воды испаряется и поднимается вверх. Сначала эти капельки такие маленькие, что их нельзя разглядеть. Потом они собираются в облака и становятся видимыми. Если облака опускаются низко над землёй, они становятся туманом. Чаще всего туманы бывают там, где много влаги — над рекой или в низинах. Обычно туманы появляются утром или вечером, когда земля остывает. Но стоит пригреть солнышку — утренний туман рассеивается. Это не значит, что он исчезает: просто он снова превращается в пар и поднимается вверх. А что происходит с вечерним туманом? Капельки воды, из которых состоит туман, опускаются на землю, прикасаются к предметам, листьям, траве и превращаются в росу. Конечно, ты видел её не раз после ясных холодных ночей. Роса, как тысячи рассыпавшихся бриллиантов, сверкает на солнце радужными искорками. А если холодно и температура воздуха ниже нуля, капельки влаги ложатся на землю маленькими кристалликами льда — инеем. Так путешествует лишь часть капелек. А что происходит с другими?
1) При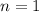 равенство примет вид
равенство примет вид  , следовательно, при
, следовательно, при 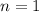 имеем верное равенство.
имеем верное равенство.
2) Предположим справедливость этого утверждения для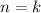 , где
, где  — произвольное натуральное число, и с учетом этого предположения установим справедливость для
— произвольное натуральное число, и с учетом этого предположения установим справедливость для 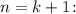
Следовательно, при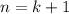 имеем истинное утверждение.
имеем истинное утверждение.
3) Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального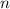 .
.