Рассмотрим 2 случая.
1. Угол 120° при вершине, КР=24 основание. Тогда к к нему проведена высота МН, которая есть и медианой, и биссектрисой. КН=12, уг КМН=60°, tg60°=12/MH, |/3=12/MH, MH=4|/3.
S =1/2 *24*4|/3 =48|/3 (ед.2)
2. Угол при вершине 120°. КР=24 боковая сторона треугольника.
Тогда S=1/2 *24^2 *sin120°=
=1/2 *24^2*(|/3 /2)=144|/3 (ед. 2).
И в первом, и во втором случаях есть ещё и другие нахождения площади. И зависит от того, какие темы вы изучали. Если не изучали предложенные формулы, то использовать теорему Пифагора и знание того, что напротив угла 30° лежит катет в 2 раза меньше гипотенузы.
Если диагональ квадрата равна 20, то сторона квадрата: a = 20/√2 = 10√2.
Найдём диаметр цилиндра: d = 8•2 = 16.
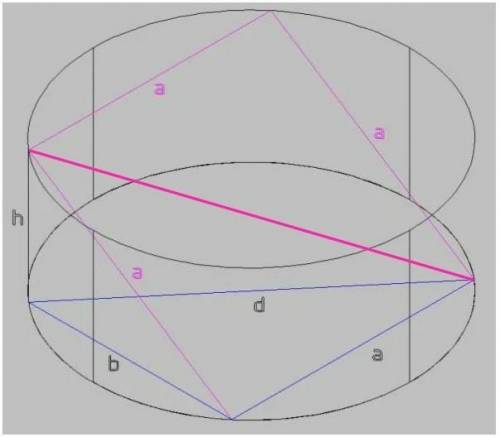
По условию плоскость квадрата АВСD не параллельна оси цилиндра. В этом случае центр квадрата совпадает с центром цилиндра.
На рисунке проекция квадрата на основание показана синим цветом.
b — проекция наклонной стороны квадрата на плоскость основания.
По теореме Пифагора: a² + b² = d² ;
b² = d² - a² = 16² - (10√2)² = 256 - 100•2 = 56;
b = √56 = 2√14.
И снова по теореме Пифагора, но уже для вертикально расположенного прямоугольного треугольника:
h² + b² = a² ;
h² = a² - b² = (10√2)² - (2√14)² = 200 - 56 = 144;
h = √144 = 12.
600/70=60д. /7д.= 8(ост 4д.) =8(ост 40)
66/70 = 60 десятков / 7 десятков = 8 ( остаток 4 десятка) = 8(ост.40)