D=2R
D1=2×3.25=6.5 cm
D2=2×4.5=9 dm
D3=2×2.57=5.14 cm
AC=10 см
Пошаговое объяснение:
Розв'язання:
Нехай дано ∆АВС, МК - серединний перпендикуляр до сторони АВ,
т. М належить сторон!і ВС, ВС = 16 см, Р∆АМС = 26 см. Знайдемо сторону АС.
Розглянемо ∆АМК i ∆BMK.
1) АК = KB (т. К - середина АВ);
2) ∟AКM = ∟BKM = 90° (МК ┴ АВ);
3) MК - спільна.
Отже, ∆АМК = ∆BMК за I ознакою, з цього випливає, що AM = MB.
Р∆АМС = АС + АМ + СМ (т.я. АМ = МВ, то Р∆АМС = АС + МВ + СМ).
26 = АС + MB + CM, MB + СМ = СВ = 16 см.
26 = АС + 16; АС = 26 - 16; АС = 10 см.
Biдповідь: AC = 10 см.
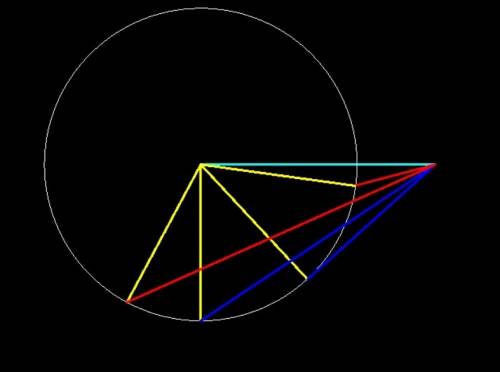
Пояснение к рисунку. Голубым цветом построен отрезок длиной 9, окружность - множество возможных положений конца отрезка длиной 6. Желтым - некоторые варианты положения отрезка длиной 6 (зеркальные не рассматриваем, чтобы не загромождать рисунок). Красным - значения а, когда треугольник становится тупоугольным (в случае малого а, тупым является угол между 6 и а, в случае большого - угол между 9 и 6). Синим цветом отрисованы граничные положения (значения а), когда
1) а становится катетом. При этом a = √9^2 - 6^2 = √81-36 = √45 = 3√5
2) а становится гипотенузой. При этом а = √9^2 + 6^2 = √81+36 = √117 = 3√13
При а между этими 2 значениями треугольник является остроугольным
3√5 < a < 3√13
Пошаговое объяснение:
d=2r
а)2*3,25=6,5 см
б) 2*4,5=9 дм
с) 2*2,57=5,14 см