Пошаговое объяснение:
Объясню на примере 2965 х 72
Сначала цифру 2 умножаем поочерёдно на все цифры верхней строчки :
2 х 5 = 10 ( 0 пишем, 1 в уме)
2 х 6 = 12 ( прибавляем 1, что был в уме = 13.... 3 пишем, 1 опять в уме)
2 х 9 = 18 ( прибавляем 1, что был в уме = 19... 9 пишем, 1 опять в уме)
2 х 2 = 4 ( прибавляем 1, что был в уме и пишем 5)
И так далее со вторым числом.
Но! Все последующие расчёты мы записываем со сдвигом на одну цифру, иначе не сойдется.
Если в множителе есть ноль, то мы не пишем нули в строчке, а просто сдвигаем строчку ещё на одну цифру!
Как на картинке. Нули можно не писать, но тогда нижняя строчка сдвинется на 2 цифры влево
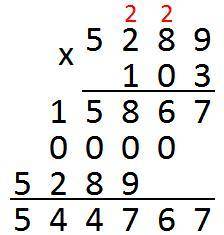
255=5*51=5*3*17
221=13*17
130*255*221=13*5*2*5*3*17*13*17=13^2*17^2*5^2*6
Sqrt(130*255*221)=13*17*5*sqrt(6)
Б)a^7=a^6*a=a*(a^3)^2
Sqrt(a^7)=модуль(a^3)*sqrt(a) так как a>0 то а^3>0 значит модуль(а^3)=(а^3)
Sqrt(a^7)=a^3*sqrt(a)
В) a^6*b^7=a^6*b^6*b=b*(a^3*b^3)^2
Sqrt(a^6*b^7)=модуль(a^3*b^3)*sqrt(b)
b>0, значит b^3>0 тоесть модуль(b^3)=b^3
Sqrt(a^6*b^7)=модуль(a^3)*b^3*sqrt(b)
Г) a/(b^6)=a/((b^3)^2)
Sqrt(a/(b^6))=модуль(1/b^3)*sqrt(a) так как b<0 то 1/b^3<0 а значит модуль(1/b^3)=-(1/b^3)
Sqrt(a/(b^6))=-(1/b^3)*sqrt(a)