Пошаговое объяснение:
В угол вписана окружность с радиусом 6 см. Расстояние от её центра до вершины угла равно 30 см. Найдите радиус меньшей окружности, которая касается сторон угла и данной окружности.
Пусть центр данной окружности будет О, точка её касания с верхней стороной угла В.
Пусть центр меньшей окружности будет С, точка касания окружностей друг с другом - М
Соединим центр О большей окружности с точкой касания.
Проведем СК ⊥ ВО.
СО=r+6
КО=6-r
Из подобия треугольников АОВ и СОК (прямоугольные с общим острым углом) следует отношение
АО:СО=ВО:КО
30:(6+r)=6:(6-r)
36+6r=180-30r
36r=144
r=144:36
r=4 cм
сори фото не могу

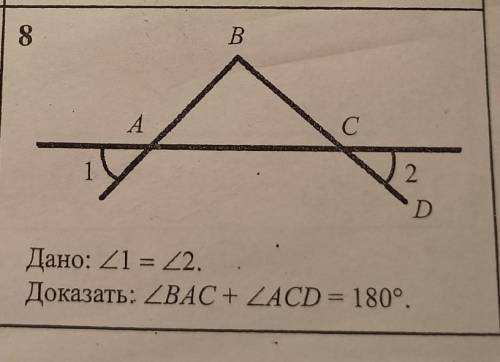
∠ВАС=∠1(накрест лежащие углы)
∠АСВ=∠2(накрест лежащие углы)
∠ВАС=∠АСВ
=>
∠АСД+∠2=180°(смежные углы в сумме дают 180°)
=>
Если ∠1=∠2=∠ВАС=∠АСВ
Значит:
∠2 можно заменить ∠ВАС и сумма углов не изменится.
Пошаговое объяснение: