Эта задача может решаться двумя геометрическим и векторным надо было указать в задании).
Геометрический.
Если мы перенесём заданный отрезок А1С1 точкой А1 в точку А, то получим плоский угол САД1 между заданными отрезками.
Решим треугольник АСД1 по теореме косинусов.
Находим длины сторон.
АС = √(4² + 8²) = √(16 + 64) = √80 = 4√5.
АД1 = √(3² + 4²) = √(9 + 16) = √25 = 5.
Д1С = √(3² + 8²) = √(9 + 64) = √73.
cos A = (80 + 25 - 73)/(2*4√5*5) = 32/(40√5) = 0,35777.
Угол А = САД1 = arc cos 0,35777 = 1,2049 радиан или 69,0366 градуса.
ответ: угол между отрезками AD1 и A1C1 равен 69,0366 градуса.
Пошаговое объяснение:
y = f(x)
множество значений, которые может принимать x, называется областью определения функции (другими словами - множество всех х, где функция существует или определена, или еще - это проекция графика функции на ось ОХ)
множество значений, которые может принимать y, называется областью значений функции (или еще проекция графика функции на ось ОУ)
нули функции - это точки х, где у(х)=0 (или точки, где график функции пересекает ось ОХ)
в нашем случае
ООФ( или D) [-3;8]
ОЗФ (или Е) [-5; 3]
нули функции х=4, х=7
Пошаговое объяснение:
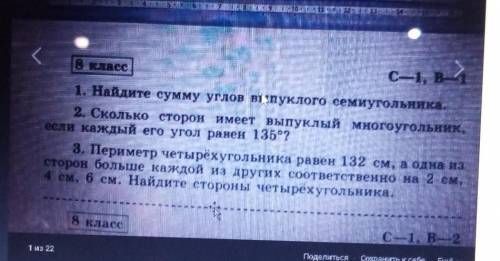
1. По формуле 180 (n-2) = 180(7-2)=180*5=900°
2. По формуле количество сторон = 360/(180-∠°)=360/(180-135)=360/45=8 (сторон)
3. Пусть большая сторона - х см, вторая - х-2, третья х-4, четвертая х-6. Периметр равен 132
х+х-2+х-4+х-6=132
4х-12=132; 4х= 144; х= 144/4; х=36 см - первая сторона 36-2=34 - вторая сторона; 36-4 = 32 - третья сторона; 36-6 = 30 - четвертая сторона.