По условию характеристические многочлены матриц второго порядка А и В совпадают. Поскольку характеристический многочлен ищется по формуле
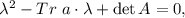делаем вывод, что
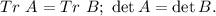
Если бы корни характеристического уравнения были бы разные, все матрицы с таким характеристическим уравнением были бы подобны, то есть были бы матрицами одного и того же оператора. Но по условию это не так. Вывод: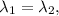 
а матрицы второго порядка с таким условием бывают двух видов: - скалярная матрица (а поскольку по условию след равен 10, это скалярная матрица 5E, где E - единичная матрица), и те, которые подобны жордановой клетке с пятерками на диагонали. Поскольку определитель матрицы (как и ее след) не зависят от выбора базиса, делаем вывод, что определители матриц А и В равны 25.
ответ: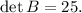 
Замечание. Зачем было путать потенциальных "решателей" и писать в условии AA и BB вместо А и В? Не понимаю.
Замечание. Tr A - это обозначение для следа матрицы, то есть суммы элементов, стоящих на главной диагонали, det A - обозначение для определителя матрицы.
Старинная русская мера массы пуд равна 16,38 кг. Округлите это значение до целых,до десятых. Старинная русская мера длины верста равна 1067м.Округлите это значение до десятков,до сотен.Старинная русская мера длины сажень равна 2,13м. Округлите это значение до целых ,до метров
Решение
(до целых) пуд равен 16,38 кг = 16 кг
(до десятых) пуд равен 16,38 кг = 16,4 кг
(до десятков) длина версты равна 1067м = 1070 м
(до сотен) длина версты равна 1067м = 1100 м
(до целых) длина сажени равна 2,13м = 2м
(до метров) длина сажени равна 2,13м = 2м
Пошаговое объяснение:
1)
1целая 4/9 + 3целых 2/7 = 1целая 28/63 + 3целых 18/63 = 4целых 46/63
2)
7целых 5/12 + 1целая 3/8 = 7целых 10/24 + 1целая 9/24 = 8целых 19/24
3)
8целых 7/20 + 4целых 19/30 = 12целых 21/60 + 4целых 38/60 = 16целых 59/60
4)
7целых 2/25 + 1целая 7/15 = 7целых 6/75 + 1целая 35/75 = 8целых 41/75