Пошаговое объяснение:
последовательность выглядит следующим образом
1,2,2,3,3,3,4,4,4,4, обозначим эту последовательность (1)
составим последовательность из количеств каждого натурального числа встречающегося в этой последовательности
то есть единиц -1, двоек-2, троек-3,...
1,2,3,4,5,6, обозначим эту последовательность (2)
заметим что сумма одного члена этой последовательности равна количеству единиц последовательности (1)
заметим что сумма двух членов этой последовательности равна количеству единиц и двоек последовательности (1)
и так далее
сумма n членов этой последовательности равна количеству чисел до n (включительно) последовательности (1)
найдем n когда сумма последовательности (2) ≈ 2016 (приближенно)
по формуле суммы арифметической прогресии
Sn=(2a₁+d(n-1))*n/2
a₁=1; d=1
Sn=(2a₁+d(n-1))*n/2=Sn=(2+n-1)*n/2=(n+1)n/2
Sn=2020
(n+1)n/2=2020
n²+n-4040=0 решим квадратное урвнение
d=1+4*4040=1661
√1661=приближенно 127
n=(-1+127)/2≈126/2=63 (рассматриваем только положительный корень)
Найдем точное значение S₆₃=(63+1)*63/2=2016
то есть с 1 по 2016-го места в последовательности (1) идут числа
от 1 до 63 а начиная с 64го места идут числа 64
S₆₄=(64+1)*64/2=2080
так как 2016<2020<2080
то на 2020 месте стоит число 64
ответ: 450; 300; 225; 180; 113.
Пошаговое объяснение:
От 100 до 999 имеются 900 чисел. (Используем "правило плюс один". Это правило используется для подсчета количества чисел в числовом ряду с учетом шага. Шаг это закономерность числового ряда. К примеру, если взять ряд чисел 1 2 3 4 5 6 7 8 9 10, то шагом является +1. Для подсчета используем простую формулу: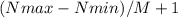 
. Где M - это шаг. 
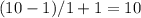, значит 10 чисел.
Теперь перейдем к пунктам.
1) При делении на 2, остаток 1.
Заметим, что от 100 до 999 число начинается с четного, а заканчивается нечетным. Это делает пример очень удобным для подсчета. Отсюда следует, что половина всех чисел это нечетные (то есть с остатком 1) ответ: 450 чисел.
2) При делении на 3, остаток 2.
Разобьем 900 чисел на группы по 3 числа
100 101 102
103 104 105
106 107 108
и так далее. Первое число при делении на 3 дает остаток 1, второе число остаток 2, а третье число нацело делится и так далее. Последнее число 999 делится нацело на 3, таким образом, заключительная группа из трёх чисел будет таким:
997 998 999. При делении 997 на 3 - остаток 1, 998 на 3 - остаток 2. Это значит, что каждое второе число в группе дает остаток 2. 900/3 = 300.
ответ: 300 чисел.
3) При делении на 4, остаток 3.
Таким же образом делим на группы по 4 числа.
100 101 102 103
104 105 106 107
108 109 110 111
и так далее.
996 997 998 999. 1-ое число делится нацело, 2-ое число - остаток 1, 3-е число - остаток 2, 4-ое число - остаток 3. 900/4 = 225.
ответ: 225 чисел.
4) При делении на 5, остаток 4.
100 101 102 103 104
105 106 107 108 109
...
995 996 997 998 999.
900/5 = 180.
ответ: 180 чисел.
5) При делении на 8, остаток 7.
Тут чуток иначе, но принцип тот же. Если посчитаем, то первое число 100 при делении на 8 выдает остаток 4. Значит у каждого последующего числа остаток будет на 1 больше, максимальный остаток - 7. Число 104 уже разделится нацело. Чтобы использовать удобный подсчет с использованием "правило +1", начнём с минимального числа, делящегося на 8 - это 104, заканчивая максимальным делящимся 8 - это 992. Подставляем в формулу: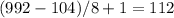 
. Теперь добавляем числа, которые не были взяты для подсчета с остатком 7, это 103 и 999. Теперь важный момент. При расчете количества чисел, мы начинали с числа, который делится нацело и заканчивали числом, тоже делящееся на 8. В последней группе чисел, начиная с 992 заканчивая 999, должно быть одно число, которое выдает остаток 7 - это 999. Значит 112 чисел от 104 до 999 и число 103. Всего 113 чисел.
ответ: 113 чисел.
5
Пошаговое объяснение: