Question

Из колоды карт (32 листа) каждому из трех игроков наудачу раздается 10 карт. Сколько различных комбинаций этого опыта возможно?

Answer 1

$C^{10}_{35}*C^{10}_{22}*C^{10}_{12}$

или

$2\,\,753\,\,294\,\,408\,\,504\,\,640$

Пошаговое объяснение:

Давайте сначала введём понятие.

Определение. Назовём числом сочетаний из n по k число выбрать из множества мощностью n элементов множество мощностью k элементов, будем обозначать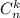 $C^k_n$ и определим формулой

$\displaystyle C^k_n=\frac{n!}{k!(n-k)!}$

Если нужно доказательство, пишите

Итак, приступаем к решению.

Сначала раздаем первому игроку.

Для него есть 32 карты, из которых мы выбираем 10. Тогда количество выбрать эти карты есть число сочетаний из 32 по 10.

$\displaystyle C^{10}_{32}=\frac{32!}{10!(32-10)!}= \frac{22!*23*24*25*26*27*...*32}{22!*10*9*8*7*6*5*4*3*2} =\\=\frac{23*24*25*26*37*...*35}{10*9*8*7*6*5*4*3*2}=64512240$

Но можно было просто оставить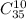 $C^{10}_{35}$

Мы уже дали 10 карт первому, поэтому осталось 32 - 10 = 22 карт.

Тогда количество раздать второму 10 карт из 22 - это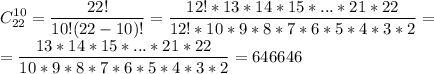 $\displaystyle C^{10}_{22}=\frac{22!}{10!(22-10)!}=\frac{12!*13*14*15*...*21*22}{12!*10*9*8*7*6*5*4*3*2}=\\=\frac{13*14*15*...*21*22}{10*9*8*7*6*5*4*3*2}=646646$

Или опять же можно было бы оставить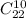 $C^{10}_{22}$

Третьему останется всего лишь 22 - 10 = 12 карт. Тогда точно также, число выбрать из 12 карт 10 равно

$\displaystyle C^{10}_{12}=\frac{12!}{10!(12-10)!}=\frac{12*11*10!}{10!*2}=66$

Ну хоть здесь нормальное число. Но опять же можно было и оставить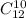 $C^{10}_{12}$

И так, для каждого из игроков есть свои варианты выбора, причем выбор другого, напрямую зависит от выбрав первого. Тогда нам необходимо перемножить все эти результаты.

Получим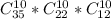 $C^{10}_{35}*C^{10}_{22}*C^{10}_{12}$

Или если в числах, то это

$64512240*646646*66=2753294408504640=2\,\,753\,\,294\,\,408\,\,504\,\,640$

Answer 2

77/6203102, из-за того что каждый может получить только 10 карт число нужно утроить, и получится 77/206770. Это примерно 0.00037.

Пошаговое объяснение:

Число раздать карты 3-м игрокам

N=C(10 из 32)*C(10 из 22 )*C(10 из 12)=32! / (10! * 10! * 10! * 2! )

Число раздать 10 картинок первому игроку

M=C(10 из 16)*C(10 из 22 )*C(10 из 12)

ответ такой же как и раньше, но по другому записан

Р= 3*M / N =3* C(10 из 16) / C(10 из 32)=3* (16!*22!)/(6! * 32!)