В классе 16 парт .
В понедельник всех 13 учеников рассаживаем на одну парту по два человека (один ученик остается без пары) , и дорисовываем свободные 9 парт .
Во вторник же чтобы вышло 6 свободных парт из того же количества мест , что и в понедельник , то нужно просто всех 10-х учеников рассадить по одному .
1) 
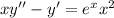
Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на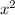 
, получаем
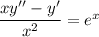
В левой части уравнения это ни что иное как формула производной частного, то есть :
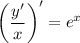
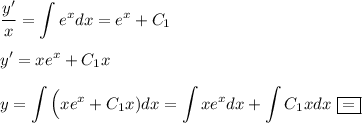
Подсчитаем отдельный интеграл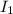 
по частям.
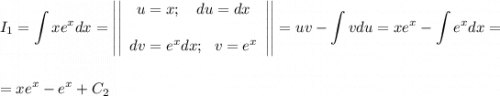
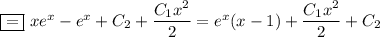
2) 
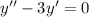
Это линейное однородное дифференциальное с постоянными коэффициентами. Замена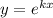 
, перейдём к характеристическому уравнению: 
, 
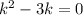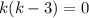корни которого 
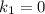и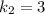 
. Тогда общее решение диф. уравнения: 
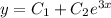и его первая производная 
.
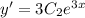Осталось найти константы C₁ и C₂ , подставляя начальные условия.
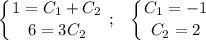
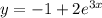— частное решение.
Пошаговое объяснение:
Как надо строить графики простых функций типа у= ах+б (1)
Меня научил очень пожилой человек - из эпохи Гагарина.
Наверное, все знают график функции у=ах, где а=1
Так вот, чтобы постоить график функции (1) надо
1. Построить как бы новую систему координат, которая
имеет координаты пересечения осей Хнов и У нов в точке = (0,в).
2. И в этой новой системе координат строим всем известный график функции у=ах, а - определяет наклон новой функции относительно у=х.
В нашем случае,
в= 2, а= -3 (т.е этот график будет в во 2 и 4- квадранте),
и наклон его будет в а раз (а=3) круче, чем у прямой у=х
16 парт ну тип получаеться 13:2=6.5 ( это получаеться 7 парт зането)
И 7 +9=16