11
Пошаговое объяснение:
121÷11=11
11^2=121
х-цена учебника,
у-цена тетради
6х+10у=205.5
8х+5у=219.5,
решая систему, получаем
учебник 23,35руб.
тетрадь 6,54руб.
ЕСЛИ НЕ ЧЕРЕЗ СИСТЕМУ ТОГДА ТАК
6 учебников и 10 тетрадей стоит 205,5 руб.
8 учебников и 5 тетрадей стоит 219,5 руб.
Произведём вторую покупку дважды! Тогда мы купим 16 учебников и 10 тетрадей на 219,5*2=439 руб.
Сравним первую и удвоенную вторую покупку
6 уч и 10 тет стоит 205,5 руб.
16 уч и 10 тет на 219,5*2=439
Таким образом, купив на 16-6 =10 уч больше мы платим больше на 439-205,5 = 233,5 руб.
Тогда 10 уч стоит 233,5 рублей.
Один уч стоит 233,5 : 10 = 23,35 руб.
Теперь найдём стоимость одной тетради: 6 * 23,35 = 140,1 рублей стоит 6 учебников
Тогда 6 учебников, которые стоят 140,1 рублей и 10 тетрадей стоит 205,5 руб
отсюда 10 тетрадей стоят 205,5-140,1 = 65,4 рублей
Отсюда одна тетрадь стоит: 65,4:10=6,54 рубля
ответ: Одна тетрадь = 6 р 54 коп, Один учебник = 23 рубля 35 копеек
Пошаговое объяснение:
I вариант решения
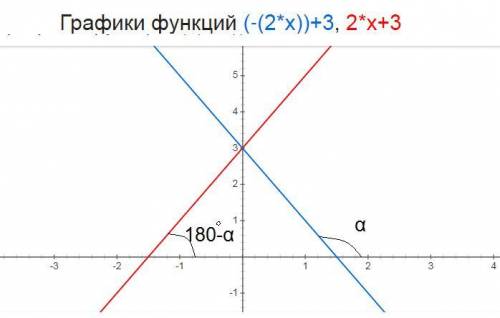
пусть прямая симметричная прямой y=-2x+3 имеет вид у=kx+b
найдем точки пересечения прямой y=-2x+3 с осями координат относительно оси ОУ
с осью ОХ у=0; -2x+3=0; 2x=3; x=1,5; (1,5;0)
с осью ОY x=0; y=3; (0;3)
так как прямые симметричны то
- они обе проходят через точку (0;3)
- симметричная прямая проходит через точку противоположную точке (1,5;0) точку (-1,5;0)
⇒ симметричная прямая проходит через точки (0;3) и (-1,5;0)
подставим координаты точки (0;3) в уравнение симметричной прямой у=kx+b координату точки (0;3)
получим 3=к*0+b; b=3
подставим координаты точки (-1,5;0) и значение b=3 в уравнение симметричной прямой у=kx+b получим
0=-1,5к+3 ; 1,5к=3; k=3/1,5=2
подставим b=1; k=2 в уравнение у=kx+b
у=2х+3
===============================================
II вариант решения - тригонометрический
так как прямые симметричны то их углы наклона к оси ОХ будут в сумме давать 180°
так как tg(180°-а)=-tga то угловые коэффициенты симметричных прямых будут к₁ и к₂ противоположными числами а значение b₁ и b₂ будут одинаковыми так как обе прямые пересекают ось ОУ в одной точке ⇒ к₂=-к₁=-(-2)=2; b₂=b₁=3
уравнение прямой симметричной прямой y=-2x+3 относительно оси ОУ
у=2х+3
121:11=11
Пошаговое объяснение: