Нет
Пошаговое объяснение:
Рассмотрим все цифри:
0, 2, 4, 5, 6, 8 - не могут быть этими цифрами, так как любое число, которое заканчивается на одно из них не будет простым
Остаётся 1, 3, 7, 9
Из них складываем пары чисел по три:
1, 3, 9 - выходят числа 139, 193, 319(не простое), 391(не простое), 913(не простое), 931(не простое). Значит, откидываем этот вариант
1, 3, 7 - 137, 173, 317, 371(не простое), 713(не простое), 731(не простое). Этот вариант тоже откидываем
1, 7, 9 - 179, 197, 719, 791(не простое), 917(не простое), 971. Не подходит
3, 7, 9 - 379, 397, 739, 793(не простое), 937, 973(не простое). И этот вариант тоже не подходит.
Значит, таких цифр не существует.
Представить число 7 в виде суммы трех натуральных слагаемых можно следующими с точностью до порядка слагаемых):
Представления первыми двумя не могут соответствовать сторонам треугольника, так как для них не выполняется неравенство треугольника. Заметим, что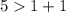
и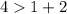 
, хотя каждая сторона треугольника должна быть меньше суммы двух других сторон.
Значит, треугольник имеет стороны 1, 3, 3 или 2, 2, 3. Каких-либо других ограничений на сторону АВ нет, поэтому она может иметь длину 1, 2 или 3.
ответ: 1, 2 или 3