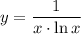 2. Область определения
2. Область определения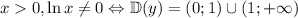 3. Область значений
3. Область значений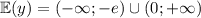 4. Нули
4. Нули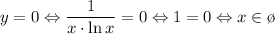 5. Разрывы
5. Разрывы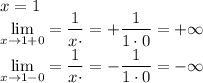
разрыв второго рода
6. Асимптотывертикальные:
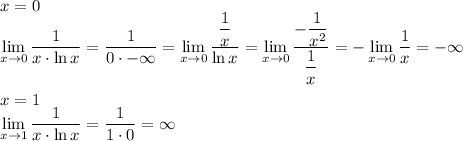
горизонтальные:
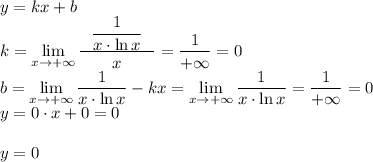 7. Экстремумы
7. Экстремумы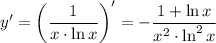
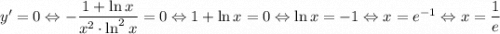
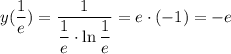
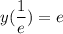 8. Промежутки возрастания - убывания
8. Промежутки возрастания - убывания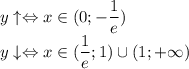 9. Точки перегиба и выпуклость функции вверх - вниз
9. Точки перегиба и выпуклость функции вверх - вниз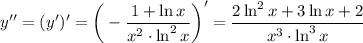
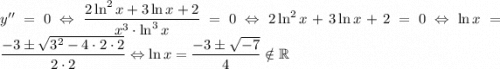
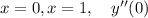 не определена (делим на 0)
не определена (делим на 0)
расставим знаки второй производной:
- 0 - 1 +
----------------------------|-------------------------------|---------------------
(не определена) (выпуклая вверх) (выпуклая вниз)
Точек перегиба нет, при 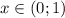 выпуклая вверх, при
выпуклая вверх, при 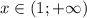 выпуклая вниз
выпуклая вниз
общего вида
11. График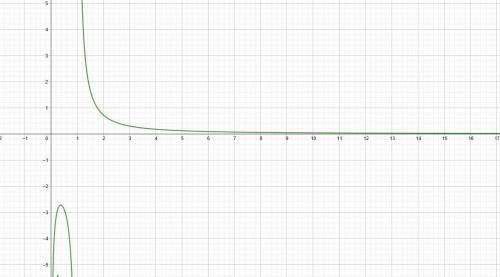
2*3,5=7м2-пол в ванной
0,15*0,15=0,0225-площадь плитки
0,0225*200=4,5м2-общая площадь купленной плитки
плитки на пол не хватает.
2:0,0225=13-плиток
3,5:0,0225=23-плитки
13*23=299-всего надо целой плитки для пола
По ширене нужно порезать 24 плитки и 13 по длине
299 целых плиток+37 для резки-200 купленной плитки=136 плиток надо купить
Кажеться так