Пошаговое объяснение:
a) табличный интеграл = arctgx + C
в подстановке 1__0 получим arctg(1) - arctg(0) = pi/4 - 0 = pi/4
б) занесу 3х + 1 под дифференциал:
d(3x+1) = 3 dx => dx = 1/3 d(3x+1) => 1/3 *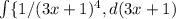 
= 1/3 * (-1/3)* 1/(3x+1)^3 + C = -1/(9*(3x+1)^3) + C
в подстановке 1__0 получим -1/(9*4^3) + 1/(9*1^3) = -1/576 + 1/9 = 63/576 = 7/64
в)занесу cosx под дифференциал:
cosx dx = d(sinx)
d(3sinx+1) = 3cosx dx => dx = 1/3cosx * d(3sinx+1)
получим 1/3*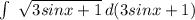 
= 1/3 * 2/3 * (3sinx + 1)^(3/2) + C
в подстановке pi/2__0 получим 2/9 * (3+1)^3/2 - 2/9*(1)^(3/2) = 16/9 - 2/9 = 14/9
г) занесу e^(-2x) под дифференциал
d(e^(-2x)) = -2*e^(-2x) dx
dx = 1/(-2*e^(-2x)) d(e^(-2x))
получим: -1/2 *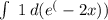 
(cтепень криво написалась) = -1/2 * e^(-2x) + C
в подстановке -1/2__0 получим -1/2 * e^(1) + 1/2* e^(0) = 1/2(1 - e)
Пошаговое объяснение:
а) разделил на 2 интеграла по разности, под первым e^(pi) - константа, поэтому получится e^(pi) * x = pi* e^(pi) - 0 ( при подстановке)
второй - табличный = sinx + C = 0 в подстановке.
ответ: pi* e^(pi)
б) занесу cosx под дифференциал
cosxdx = d ( sinx + 1)
дальше простой степенной интеграл = 1/3*(1+sinx)^3 + C = 1/3 * (1)^3 - 1/3 * (1)^3 = 0
в) опять под дифференциал
d(4-t^2) = -2*t dt => tdt = -1/2 * d(4-t^2)
дальше простой степенной интеграл = -1/2*2*(4-t)^(1/2) + C = -3^(1/2) + 4^(1/2) = 2 -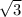 
г) под дифференциал:
d(1 + 4x^3) = 12x^2 dx => 6x^2dx = 1/2 d(1+4x^3)
дальше табличный интеграл = 1/2 * ln(1+4x^3) + C = 1/2*ln5 - 1/2*ln1 = 1/2*ln5
Пошаговое объяснение:
x/12 - 1/X
X равно 4 5 6
Подставим значение х в выражение
x/12 - 1/X = 4/12 - 1/4= 4/12 - 3/12= 1/12
x/12 - 1/X = 5/12 - 1/5= 5*5/12*5 - 1*12/5*12= 25/60 - 12/60= 13/60
x/12 - 1/X = 6/12 - 1/6= 6/12 - 2/12= 4/12 = 1/3