Дано: Решение:
S = 9 км Так как велосипедисты двигаются навстречу
v₁ = 400 м/мин = 24 км/ч друг другу, то скорость сближения:
t = 10 мин = 1/6 ч v = v₁ + v₂
Время до встречи велосипедистов:
Найти: v₂ - ? t = S/v = S/(v₁+v₂)
Тогда: v₂ = S/t - v₁ = 9 : 1/6 - 24 = 54 - 24 = 30 (км/ч)
ответ: скорость второго велосипедиста 30 км/чю
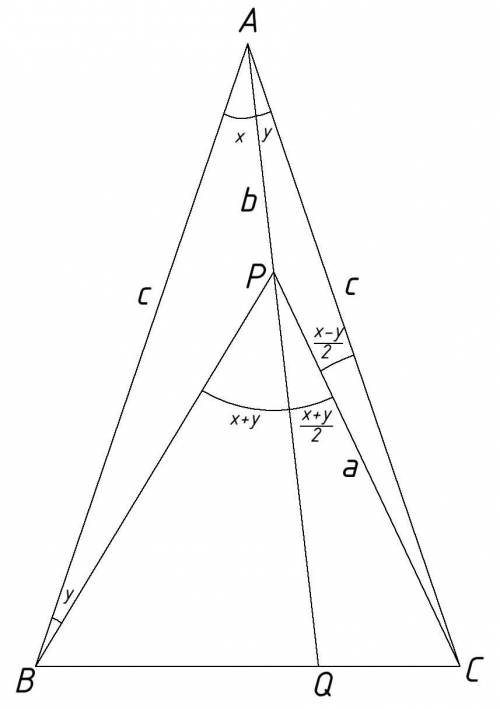
Все обозначения смотри на рисунке.
Из рассуждений суммы углов треугольника и смежных углов получаем что:
∠BPQ=x+y
∠QPC=(x+y)/2
По тем же рассуждениям можно получить,что:
∠PCA=(x-y)/2
Так же сразу отметим что:
∠CPA=180-(x+y)/2 → sin∠CPA=sin(180-(x+y)/2)=sin ( (x+y)/2 )
∠BPA=180-(x+y) → sin∠BPA=sin(x+y)
Это пригодится нам в дальнейшем.
Очевидно, что площади треугольников:
SΔBAQ/SΔQAC=BQ/QC ,тк они имеют общую высоту.
Тогда:
1/2 *c*b*sin(x)/ (1/2 *c*b*sin(y) )=BQ/QC
sin(x)/sin(y)=BQ/QC
Запишем теоремы синусов для ΔBAP и ΔPAC:
1)c/sin(x+y)=b/sin(y)
2)c/sin( (x+y)/2)=a/sin(y)
3) a/sin(y)=b/sin(x-y)/2 → a/b=sin(y)/sin ((x-y)/2)
Поделим 2) на 1)
sin(x+y)/sin ( (x+y)/2)=a/b
Откуда:
sin(x+y)/sin ( (x+y)/2)=sin(y)/sin ((x-y)/2)
2*sin( (x+y)/2 )*cos( (x+y)/2) /sin( (x+y)/2)=sin(y)/sin ((x-y)/2)
2*cos( (x+y)/2)=sin(y)/sin( (x-y)/2)
2*cos( (x+y)/2) * sin( (x-y)/2)=sin(y)
Применяем формулу произведения синуса на косинус:
2*1/2 *( sin( (x+y)/2 + (x-y)/2 ) +sin( (x-y)/2 -(x+y)/2 ) )=sin(y)
sin(x)-sin(y)=sin(y)
sin(x)=2*sin(y)
sin(x)/sin(y)=2
BQ/QC=sin(x)/sin(y)=2
Таким образом:
BQ=2*QC
ЧТД.
ОА и ОВ - радиусы окружности. Касательная всегда перпендикулярна радиусу, проведенному в точку касания. Тр-ник АОВ равнобедренный, АВ-основание, углы приосновании равны (180-146)/2=17. Угол между АВ и касательной равен 90-17=73.