Обозначим радиус основания цилиндра - R
Высоту цилиндра обозначим через H
Тогда объём цилиндра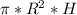 
= V, площадь поверхности цилиндра
S =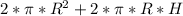 
Первый раз решаю, поэтому подробно. выразим из уравнения объёма H и подставим его в функцию площади поверхности цилиндра.
H =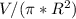 
S =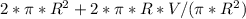 
S =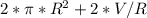 
Найдём точки экстремума для функции S(R), найдя нули её производной
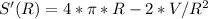
S'(R) принимает значение 0 только в одной точке.
R0 = \![\sqrt[3]{V/(2*\pi)}](/tpl/images/0000/6545/cc02d.png)
Слева от точки R0 функция S(R) убывает, а справа Возрастает. Точка R0 минимум функции S(R).
ответ. R0 = \
H = V/(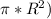
Зачем здесь объяснять