Даны координаты четырех точек А(1,-1,4), В(2,0,-3), С(1,-1,5), D(3,2,-4). Найти: 3) составить уравнение - id1426864920200424 от peskovavikulya 24.04.2020 17:19

Question

Математика: Даны координаты четырех точек А(1,-1,4), В(2,0,-3), С(1,-1,5), D(3,2,-4). Найти: 3) составить уравнение прямой, проходящей через точку D а) параллельно прямой АВ б) перпендикулярно прямой АВ 4) уравнение плоскости, проходящей через точку Д, перпендикулярно прямой АВ

peskovavikulya · Accepted Answer

Разделим обе части указанного неравенства на положит. число a^3 и сделаем замену переменной: t = b/a > 0:

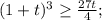
$(1+t)^3\geq\frac{27t}{4};$

Раскроем куб суммы и домножив на 4, получим:

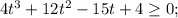
$4t^3+12t^2-15t+4\geq0;$

Многочлен в левой части раскладывается на множители по стандартной процедуре. Подбором устанавливается целый корень: -4, далее делением многочлена на (t+4) получим (2t-1)^2 и полное разложение имеет вид:

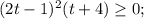
$(2t-1)^2(t+4)\geq0;$

Видим, что при t>0 указанное неравенство верно, что и требовалось доказать.

Равенство 0 достигается при t = 1/2, то есть при любых положительных a и b, отвечающих условию: a = 2b

MOGZ ответил