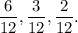
Наименьший общий знаменатель - это наименьшее положительное число кратное знаменателям данных дробей.
По-другому, нам нужно найти НОК (наименьшее общее кратное) чисел 2, 4 и 6.
Разложим каждое из этих чисел на простые множители.2 = 2.
4 = 2 * 2.
6 = 2 * 3.
Запишем разложение большего из чисел и дополним его теми множителями из остальных разложений, которых ещё не хватает в записанном произведении и вычислим:НОК (2, 4 и 6) = 2 * 3 * 2 = 12.
Значит наименьший общий знаменатель данных дробей это 12.
Разделим общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель.12 : 2 = 6
12 : 4 = 3
12 : 6 = 2
Умножим числитель и знаменатель каждой дроби на её дополнительный множитель.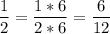
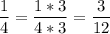
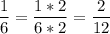
Радиус r вписанной окружностиr = 4 см.
Радиус R описанной окружности = 8,125 см.
Пошаговое объяснение:
3.Дан треугольник АВС, высота ВД=12 см, АД=5 см, ДС=9 см.
Сторона АС = 5 + 9 = 14см.
Отсюда находим площадь треугольника.
S = (1/2)*АС*h = (1/2)*14*12 = 84 см².
Теперь используем формулы радиуса.
Радиус r вписанной окружности равен отношению площади треугольника к его полупериметру.
Находим неизвестные стороны.
АВ = √(5² + 12²) = √(25 + 144) = √169 = 13 см.
ВС = √(9² +12²) = √(81 + 144) = √225 = 15 см.
Полупериметр р = (13 + 15 + 14)/2 = 42/2 = 21 см.
Находим: r = S/p = 84/21 = 4 см.
Радиус R описанной окружности равен:
R = abc/(4*S) = 13*15*14/(4*84) =2730/336= 8,125 см.