x+y= (x-y)*2
Пусть x=6, а y=2, тогда 6+2=(6-2)*2
x^2 + y^2
6^2+2^2=36+4=40
6*2=12
40 - 100%
12 - x%
(12*100)/40= 30%
100%-30%=70%
ответ: на 70% квадрат суммы этих чисел больше их произведения.
а) Доказательство в объяснении.
б) Площадь сечения равна 18√2 ед².
Пошаговое объяснение:
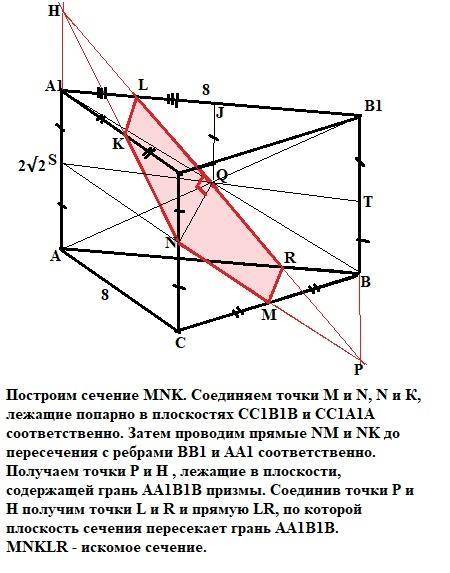
Для начала построим сечение MNK. Соединяем точки M и N, N и К, лежащие попарно в плоскостях СС1В1В и СС1А1А соответственно. Затем проводим прямые NM и NK до пересечения с ребрами ВВ1 и АА1 соответственно. Получаем точки Р и Н , лежащие в плоскости, содержащей грань АА1В1В призмы. Соединив точки Р и Н получим точки L и R и прямую LR, по которой плоскость сечения пересекает грань АА1В1В. MNKLR - искомое сечение.
а) Теперь надо доказать, что прямая LR проходит через точку Q.
Точка пересечения диагоналей - центр прямоугольника АА1В1В, следовательно, прямая ST, проходящая через середины сторон АА1 и ВВ1, параллельная АВ и А1В1, проходит через точку Q.
Тогда в равных по двум катетам (SH = ТР и SQ = TQ) прямоугольных треугольниках SHQ и TPQ отрезки A1L и BR равны, как соответственные средние линии. Треугольники QA1L и BRQ равны по двум сторонам (QA1=QR - A1B диагональ прямоугольника А1L = BR) и углу между ними (∠LA1Q = ∠RBQ, как накрест лежащие углы при параллельных АВ и А1В1 и секущей А1В).В равных углах против равных сторон лежат равные углы. Значит ∠А1QL = BQR. А так как А1В - прямая, то ∠А1QL и BQR - вертикальные и по определению LR - прямая, проходящая через точку Q. Следовательно, сечение проходит через точку Q и точки Q, M, N и K лежат в плоскости сечения, что и требовалось доказать.
б) Отметим, что ∠LQN = RQN = 90° так как QN параллельна плоскости основания, а плоскость АА1В1В перпендикулярна плоскости основания. KL║NQ║MR.
Тогда QNKL и QNMR - равные прямоугольные трапеции.
В трапеции NKLQ основания NQ = (√3/2)·a (как высота правильного треугольника) NQ = (√3/2)·8 = 4√3 ед.
KL = (1/2)·NQ = 2√3 ед. (средняя линия треугольника NHQ).
LQ = √(LJ²+JQ²) = √(4+2) = √6 ед. (по Пифагору).
Площадь трапеции Snklq = (KL+NQ)·LQ/2 = (2√3+4√3)·√6/2 = 9√2 ед².
Тогда Snklrm = 2·Snklq = 18√2 ед².
Пошаговое объяснение:
воспользуемся предельным признаком сравнения
для этого для нашей функции f(x) найдем удобную функцию g(x), сходимость интеграла которой известна, и найдем
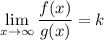
и тогда, если к≠ 0, то несобственные интегралы от этих функций функции ведут себя одинаково
как правило в качестве g(x) выбирают степенную функцию, т.к. известно, что
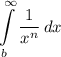сходится при n > 1, и расходится при n ≤ 1
итак наша функция f(x) эквивалентна функции g(x)
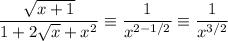
теперь предел
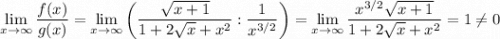
следовательно несобственный интеграл f(x) ведет себя также как несобственный интеграл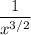 
, т.е сходится.
число --- 100%
0.5*число --- 50%
на 50% больше --- число+0.5*число = 1.5*число
x+y = 1.5(x-y) --- x^2 + y^2 = k * xy
(x+y)^2 = 1.5*1.5*(x-y)^2
x^2 + 2xy + y^2 = 1.5*1.5*(x^2 - 2xy + y^2) = 1.5*1.5*(x^2 + y^2) - 1.5*1.5*2xy
2xy + 1.5*1.5*2xy = 1.5*1.5*(x^2 + y^2) - (x^2 + y^2)
(1 + 1.5*1.5)*2xy = (1.5*1.5 - 1)*(x^2 + y^2) = (1.5 - 1)*(1.5 + 1)*(x^2 + y^2)
6.5*xy = 1.25*(x^2 + y^2)
x^2 + y^2 = xy * 6.5/1.25 = 5.2 * xy
k = 5.2
ответ: на 420 %