1. Раскладываем оба числа на простые множители:
18=2*3*3=2*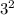
27=3*3*3=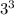
2. Для нахождения НОК берем каждое число в наибольшей степени (т.е. у числа 18 есть два множителя это 2 в первой степени и 3 во второй степени, а у числа 27 есть только один множитель это 3 в третьей степени, поэтому берем 2 в первой степени и 3 в третьей степени):
НОК (27,18)=2*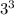 =54
=54
Проверка:
54/18=3
54/27=2
Відповідь:
у=2х² + 4х - 6.
Покрокове пояснення:
це парабола - загальне рівняння параболи:
ах²+bх+c=0
знайдемо с, то точка , де парабола перетинається з віссю ординат (0;-6)
с= - 6
вітки параболи направлені вгору , це означає , що а> 0 ;
парабола звужена на 1 одиницю вдвічі, це означає, що a=2
По координатам вершини (-1,8) запишемо рівняння до загального рівняння у= 2( х--х0)²-у0, де (х0;у0) координати вершини
у=2(х-(-1))²-8
у=2(х+1)²-8
у=2(х²+2х+1) -8
у=2х² + 4х- +2-8
у=2х² + 4х - 6.
Перевіремо, чи токи перетину графіку з асцисами є коренями рівняння: (-3;0) та (1;0)
у(-3)=2*9-12-6=0
у(1)=2*1+4-6=0
Рівняння записано вірно у=2х² + 4х - 6.
Відповідь:
у=2х² + 4х - 6.
Покрокове пояснення:
це парабола - загальне рівняння параболи:
ах²+bх+c=0
знайдемо с, то точка , де парабола перетинається з віссю ординат (0;-6)
с= - 6
вітки параболи направлені вгору , це означає , що а> 0 ;
парабола звужена на 1 одиницю вдвічі, це означає, що a=2
По координатам вершини (-1,8) запишемо рівняння до загального рівняння у= 2( х--х0)²-у0, де (х0;у0) координати вершини
у=2(х-(-1))²-8
у=2(х+1)²-8
у=2(х²+2х+1) -8
у=2х² + 4х- +2-8
у=2х² + 4х - 6.
Перевіремо, чи токи перетину графіку з асцисами є коренями рівняння: (-3;0) та (1;0)
у(-3)=2*9-12-6=0
у(1)=2*1+4-6=0
Рівняння записано вірно у=2х² + 4х - 6.
54
Пошаговое объяснение:
Легко сделать так. 27 увеличеваешь в два раза, получается 54, смотришь, делится оно на 18, раз делится, это я есть НОК чисел