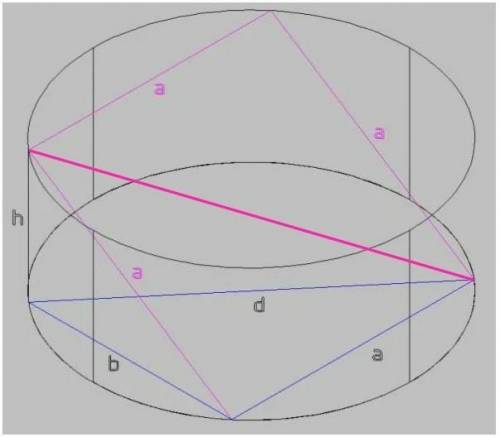
Если диагональ квадрата равна 20, то сторона квадрата: a = 20/√2 = 10√2.
Найдём диаметр цилиндра: d = 8•2 = 16.
По условию плоскость квадрата АВСD не параллельна оси цилиндра. В этом случае центр квадрата совпадает с центром цилиндра.
На рисунке проекция квадрата на основание показана синим цветом.
b — проекция наклонной стороны квадрата на плоскость основания.
По теореме Пифагора: a² + b² = d² ;
b² = d² - a² = 16² - (10√2)² = 256 - 100•2 = 56;
b = √56 = 2√14.
И снова по теореме Пифагора, но уже для вертикально расположенного прямоугольного треугольника:
h² + b² = a² ;
h² = a² - b² = (10√2)² - (2√14)² = 200 - 56 = 144;
h = √144 = 12.
3)все 4 функции вида y = kx + b. если b > 0, то прямая соприкасается с осью ординат выше оси абсцисс, а если b < 0, то прямая соприкасается с осью ординат ниже оси абсцисс. значит, графики a и b соответствуют уравнениям 2 и 3, а графики c и d соответствуют уравнениям 1 и 4. определим теперь конкретно какой график к какому уравнению подходит. рассмотрим уравнение, в котором k = 2 y = 2x + 5, причём x = = 2,5. значит, прямая проходит через точку абсцисс 2,5. рассмотрим уравнение, в котором k = 1 y = x - 5, из свойств числового коэффициента b следует, что график проходит через точку ординат -5, а из формулы y = a(x - m)² следует, что точка соприкосновения оси абсцисс и прямой смещена вправо на 5. проведя аналогичные рассуждения с остальными двумя уравнениями и их графиками, придём к выводу, что1) - c2) - a3) - b4) – d