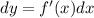 или
или 

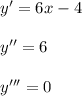


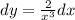
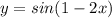




317
Пошаговое объяснение:
Пусть искомое трёхзначное число содержит х сотен, у десятков и z единиц. Произведём его разложение по разрядам: 100 ∙ х + 10 ∙ у + z.
По условию задачи известно, что сумма его цифр (х + у + z) равна разности между числом 328 и искомым числом.
Составим уравнение с тремя неизвестными:
х + у + z = 328 – (100 ∙ х + 10 ∙ у + z)
х + у + z + 100 ∙ х + 10 ∙ у + z = 328
101 ∙ х + 11 ∙ у + 2 ∙ z = 328.
Данное уравнение решим методом подбора.
1. Чтобы искомое число можно было вычесть из числа 328, для числа сотен должно выполняться ограничение: 1 ≤ х ≤ 3. Пусть х = 3, тогда:
101 ∙ 3 + 11 ∙ у + 2 ∙ z = 328
11 ∙ у + 2 ∙ z = 328 - 303
11 ∙ у + 2 ∙ z = 25
2. Для числа десятков должно также выполняться ограничение: 1 ≤ у ≤ 2. Пусть у = 2, тогда 2 ∙ z = 3 и z = 1,5 (неоднозначное число) – не удовлетворяет условию задачи. Пусть у = 1, тогда:
11 ∙ 1 + 2 ∙ z = 25
2 ∙ z = 14
z = 7
317 - искомое число.
Проверим:
328 - 317 = 11
Сумма цифр числа 317: 3 + 1 + 7 = 11
Сумма цифр числа 317 равна разности между числом 328 и исковым числом 317 .
V = S/t V = n/4. V = d/t.
n/4 = d/t t = 4d/n