Question

Найти сумму корней(или корень, если он один) уравнения $x^{4}-15x^{2} -2x^{3}+12x +36=0$

Answer 1

В левой части уравнения можно применить группировку с некоторыми слагаемыми и вынести за скобки общий множитель.

$x^4-2x^3-15x^2+12x+36=0\\ \\ x^2(x^2-2x-15)+12(x+3)=0\\ \\ x^2(x+3)(x-5)+12(x+3)=0\\ \\ (x+3)(x^3-5x+12)=0\\ \\ x_1=-3\\ \\ x^3-5x+12=0$

По т. Виета кубического уравнения: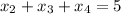 $x_2+x_3+x_4=5$. Итого получаем сумму корней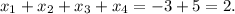 $x_1+x_2+x_3+x_4=-3+5=2.$

ДЛЯ ПОЛНОТЫ

Можно ещё продолжить решение кубического уравнения методом разложения на множители. Для этого нужно добавить и вычитать одинаковые слагаемые.

$x^3-2x^2-3x^2+6x-6x+12=0\\ x^2(x-2)-3x(x-2)-6(x-2)=0\\ (x-2)(x^2-3x-6)=0\\ x_2=2\\ \\ x^2-3x-6=0\\ x_3+x_4=3$