Пусть второй рабочий за час собирает х деталей, тогда первый собирает (х + 16) деталей в час.
Первый рабочий выполняет заказ за 105 / (х + 16)ч, а второй за 105 /х.
Зная, что второй медленнее первого на 4 ч, составим и решим уравнение:
105 / (х + 16) + 4 = 105/х.
(105 + 4х + 64 ) / ( х + 16) = 105/х.
105х + 1680 = 41х + 4х ^ 2.
4х ^ 2 - 64х -1680 = 0.
Сокращаем все на 4:
Х ^ 2 - 16х - 420 = 0.
Х1 = 20.
Х2 не подходит.
Следовательно, второй рабочий соберет 20 деталей.
ответ: 20 деталей.
Вроде бы так.
периметр = сумма длин всех сторон.
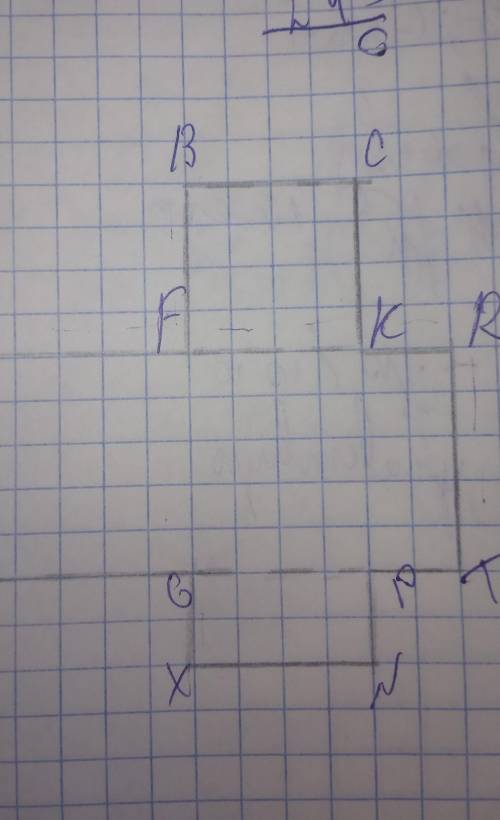
можно мысленно провести линию и поделить данную фигуру на квадрат и 2 прямоугольника, т.е. см. прикрепленный файл.
тогда => P квадрата = a * 4; P прям-ка = (a + b) * 2
=>
P фигуры = P прям-ка(1) + P прям-ка(2) + P квадрата = P = (2*4)+(6+2)*2+(1+4)*2 = 34 км
площадь = численная хар-ка двумерной геометрической фигуры.
S прям-ка = a * b; S квадрата = a * a =>
S фигуры = S квадрата + S прям-ки(1) + S прям-ки(2) = S = (2*2)+(6*2)+(1*4) = 18 км²
ОТВЕТ: S = 18 км²; P = 34 км.
1) Пара (1; 2) не подходит ко 2 уравнению.
3*1 - 2*2 + 2 = 3 - 4 + 2 = 1
Пара (-3; -1) не подходит к 1 уравнению.
2(-3) - (-1) = -6 + 1 = -5
Пара (2; 4) подходит к обоим уравнениям.
2*2 - 4 = 4 - 4 = 0
3*2 - 2*4 + 2 = 6 - 8 + 2 = 0
ответ: (2; 4)
2) Пара (1; 2) не подходит ко 2 уравнению.
5*1 - 2*2 + 1 = 5 - 4 + 1 = 2
Пара (-3; -1) не подходит к 1 уравнению.
2(-3) - 1 - 4 = -6 - 5 = -11
Пара (2; 4) не подходит к 1 уравнению.
2*2 + 4 - 4 = 4 + 0 = 4
Очевидно, в условии опечатка во 2 уравнении. Должно быть так:
{ 2x + y - 4 = 0
{ 5x - 2y - 1 = 0
Тогда пара (1; 2) подходит к обоим уравнениям.
2*1 + 2 - 4 = 2 + 2 - 4 = 0
5*1 - 2*2 - 1 = 5 - 4 - 1 = 0
ответ: (1; 2)