4/9 ≈ - 0.4444444444444444
Пошаговое объяснение:
Найдем вектор по координатам точек:
AB = {Bx - Ax; By - Ay; Bz - Az} = {4 - 2; 4 - 3; -1 - 1} = {2; 1; -2}
AD = {Dx - Ax; Dy - Ay; Dz - Az} = {-2 - 2; -1 - 3; -1 - 1} = {-4; -4; -2}
Найдем скалярное произведение векторов:
AB · AD = ABx · ADx + ABy · ADy + ABz · ADz = 2 · (-4) + 1 · (-4) + (-2) · (-2) = -8 - 4 + 4 = -8
Найдем длины векторов:
|AB| = √ABx2 + ABy2 + ABz2 = √22 + 12 + (-2)2 = √4 + 1 + 4 = √9 = 3
|AD| = √ADx2 + ADy2 + ADz2 = √(-4)2 + (-4)2 + (-2)2 = √16 + 16 + 4 = √36 = 6
Найдем угол между векторами:
cos α = AB · AD
|AB||AD|
cos α = -8
= - 4 9 ≈ - 0.4444444444444444
3 · 6
32·π см²
Пошаговое объяснение:
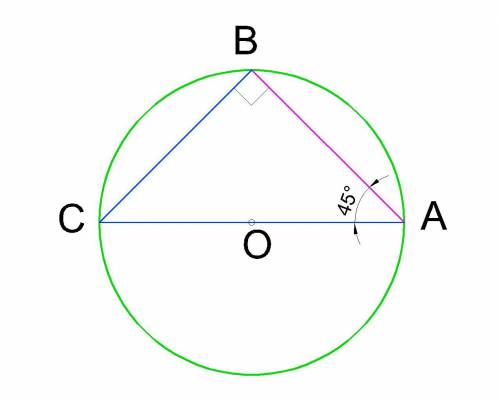
Сечение шара плоскостью представляет собой окружность.
Рассмотрим проекцию шара и секущей его плоскости на плоскость, перпендикулярную плоскости сечения.
Она представляет собой окружность, с диаметром АС= 16 см и хордой АВ (проекцией сечения плоскостью), между которыми угол 45°.
Как известно, любой треугольник построенный на диаметре окружности, третья вершина которого лежит на этой окружности является прямоугольным. Тогда ΔАВС - прямоугольный с углом при гипотенузе 45°, а катет АВ - есть диаметром сечения.
Найдем АВ: АВ=АС·cos45°=16·√2÷2 = 8√2см
Найдем площадь сечения - окружности с диаметром 8√2см:
S=πD²/4= 32·π см²