Найдем сначала общее решение соответствующего однородного дифференциального уравнения
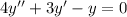
Пусть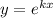 
, мы получим характеристическое уравнение
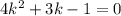
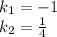
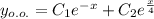— общее решение однородного диф. ур.
Найдём теперь частное решение. Рассмотрим функцию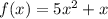 
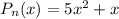отсюда 
; 
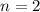. Сравнивая 
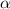с корнями характеристического уравнения и, принимая во внимая, что , частное решение будем искать в виде:
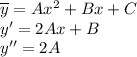
Подставляем в исходное дифференциальное уравнение
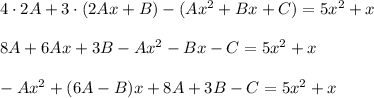
Приравниваем коэффициенты при степени x
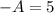откуда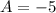 
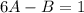откуда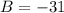 
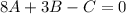откуда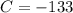 
Частное решение: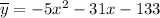 
Общее решение линейного неоднородного дифференциального уравнения:
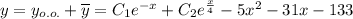
Пошаговое объяснение:
1 Частные производные для F(x,y,z)=1
dFx=2x, dFy=-2y, dFz=-2z
Значения частных производных в заданной точке - это координаты вектора нормали для касательной плоскости N=(2,4,-4)
Уравнение плоскости A*x+B*y+C*z+D=0
A=Nx=2 B=Ny=4 C=Nz=-4
D=-(Nx*Mx+Ny*My+Mz*Mz)=-(2*1+4*(-2)+(-4)*2)=14
Плоскость 2x+4y-4z+14=0
Нормаль (x-1)/2=(y+2)/4=(2-z)/4
2 Частные производные для F(x,y,z)=2
dFx=2xz-2y^3, dFy=-6xy^2, dFz=12z^3+x^2
Значения частных производных в заданной точке - это координаты вектора нормали для касательной плоскости N=(0,-6,13)
Уравнение плоскости A*x+B*y+C*z+D=0
A=Nx=0 B=Ny=-6 C=Nz=13
D=-(Nx*Mx+Ny*My+Mz*Mz)=-(0*1+(-6)*1+13*1)=-7
Плоскость -6y+13z-7=0
Нормаль (1-y)/6=(z-1)/13
3. Производные на вложенном изображении.
Чтобы перейти к целым числам значения производных в т (1,1,1) домножены на 6.
Вектор нормали тогда N=(3,5,38)
Уравнение плоскости 3x+5y+38z-46=0
Нормаль (x-1)/3=(y-1)/5=(z-1)/38
2м=200см
200:2=100см
100+40=140см
200-140=60см
первый часть 140см, вторая часть 60см.