
Пошаговое объяснение:
1.1 Прочертим диагональ и получим треугольник со сторонами 8,3 и углом между ними 120°
По теореме косинусов можем вычислить диагональ(третью сторону)
a²=b²+c²-2bc*cos120
a²=64+9-2*8*3*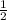
a²=49
a=7
Диагональ равна 7
1.2 Sпараллелограмма=h*a
Проведем высоту к сторону равной 8
угол между высотой и меньшей стороной будет 120-90=30, а значит мы получаем прямоугольный треугольник с углом в 30° и гипотенузой равной 3
Следовательно сторона напротив угла в 30°=3/2=1,5
По теореме Пифагора находим высоту
9=h²+2,25
h=2,5
Sпараллелограмма=2,5*8=20
2. Тут понадобится теорема синусов
(8√2)/(sin45)=(8√3)/(sinx)
sin45=√2/2
(8√2)/(√2/2)=16 ⇒ (8√3)/(sinx)=16
sinx=(8√3)/16=√3/2
sinx=√3/2 ⇒ x=60°
∠D=60°
3. Sсектора=(πR²*α)/(360)
В правильном шестиугольнике a=R⇒R=6
α=60
Sсектора=(36*60π)/(360)
Sсектора=6π≈18,84
4. АВ=√18
BC=√((-1-(-5))²+(-5-(-1))²)=√32
СD=√18
AD=√((2-(-2)²+(-2-2)²)=√32
Из этих вычислений следует то, что ABCD параллелограмм
Если AC²=AB²+BC²=AD²+CD² ,то ABCD прямоугольник
AC=√50
(√50)²=(√18)²+(√32)²
50=18+32⇒ABCD прямоугольник
5. Уравнение окружности это
(x-xцентра)²+(y-yцентра)²=R²
(x+7)²+(y-1)²=81
Центр окружности в точке (-7;1); R=9
При параллельном переносе на {3;-8} центр окажется в точке (-4;-7); радиус не изменится, значит уравнение будет выглядить вот так
(x+4)²+(y+7)²=81
4.
4x ² -16y ² при условии 2x-4y=1, 2x+4y=8.
2x-4y=1
2x+4y=8
2х=1+4у
1+4у+4у=8
1+8у=8
8у=7
у=7/8
2*х=1+4*(7/8)
2х=1+3,5
2х=4,5
х=2,25
4*2,25²-16*(7/8)² = 4*5,0625 - 16* (49/64) = 20,25 - 49/4 = 20,25-12,25 = 8
5.
x ² - 6xy + 9y ² при условии, что x+3y=3, x-3y=-1.
(х-3у)²
x+3y=3
x-3y=-1
х=3-3у
3-3у-3у=-1
3-6у=-1
-6у=-4
у=4/6
у=2/3
х=3-3*(2/3) = 1
(х-3у)² = (1-3*2/3)² = (1-2)² = -1² = 1
6.
16a ² -24ab+9b ² -4a+3b ² при условии 4a=3b
16a ² -24ab+9b ² -4a+3b ² = 16а²-24аb+12b² -4a= 4*(4a²-6ab+3b²-a)
4a=3b ⇒ a= 3b/4
4*(4a²-6ab+3b²-a) =
= 4*(4*(3b/4)²-6*(3b/4)*b+3b²-(3b/4)) =
= 4*(4*(9b²/16)-(3*3b²/2) +3b² - (3b/4)) =
= 4*(9b²/4 - 9b²/2 + 3b² - 3b/4) =
= 9b² - 18b² + 12b² - 3b = 3b²-3b = 3b(b-1)