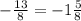х=-116/11
Пошаговое объяснение:
(0,4х+0,87)+2, 61-0,07х=0
0,4х+0,87+2,61-0,07=0
0,33х+0,87+2,61=0
0,33х+3,48=0
0,33х=-3,48
х=-116/11
63.
Пошаговое объяснение:
Рассмотрим все пары натуральных чисел, удовлетворяющих условию m+n=16:
1) 1 и 15 взаимно простые, произведение 1•15 = 15;
2) 2 и 14 не являются взаимно простыми, (например, имеют общий делитель 2);
3) 3 и 13 взаимно простые, произведение 3•13 = 39;
4) 4 и 12 не являются взаимно простыми, (например, имеют общий делитель 2);
5) 5 и 11 являются взаимно простыми, произведение 5•11 = 55;
6) 6 и 10 не являются взаимно простыми, (например, имеют общий делитель 2);
7) 7 и 9 являются взаимно простыми, произведение 7•9= 63;
8) Пара 8 и 8 не удовлетворяет условию, слагаемые не являются взаимно простыми, (например, имеют общий делитель 2)
Остальные пары чисел будут отличаться лишь порядком следования и были рассмотрены.
Наибольшее произведение слагаемых 7 и 9 равно 7•9= 63.
Приведем примерный алгоритм получения необходимых данных.
1.Нахождение области определения функции
Определение интервалов, на которых функция существует.
!!! Очень подробно об области определения функций и примеры нахождения области определения тут.
2.Нули функции
Для вычисления нулей функции, необходимо приравнять заданную функцию к нулю и решить полученное уравнение. На графике это точки пересечения с осью ОХ.
3.Четность, нечетность функции
Функция четная, если y(-x) = y(x). Функция нечетная, если y(-x) = -y(x). Если функция четная – график функции симметричен относительно оси ординат (OY). Если функция нечетная – график функции симметричен относительно начала координат.
4.Промежутки знакопостоянства
Расстановка знаков на каждом из интервалов области определения. Функция положительна на интервале - график расположен выше оси абсцисс. Функция отрицательна - график ниже оси абсцисс.
5. Промежутки возрастания и убывания функции.
Для определения вычисляем первую производную, приравниваем ее к нулю. Полученные нули и точки области определения выносим на числовую прямую. Для каждого интервала определяем знак производной. Производная положительна - график функции возрастает, отрицательна - убывает.
6. Выпуклость, вогнутость.
Вычисляем вторую производную. Находим значения, в которых вторая производная равна нулю или не существует. Вторая производная положительна - график функции выпукл вверх. Отрицательна - график функции выпукл вниз.
7. Наклонные асимптоты.
Пример исследования функции и построения графика №1
Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пошаговое объяснение:
1) 0,8х + 1,74 + 2,61 - 0,07х = 0
0,8 х - 0,07 = -1,74 - 2,61
0,73х = -4,35
х = -4,35 : 0,73
х = -5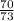
2) 6у - 8у =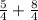
-2у =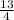
у =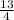 : (-2)
: (-2)
у =