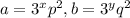, где p и q - натуральные числа, не делящиеся на 3. Ясно, что x<n, y<n. Если x=y, то, разделив обе части на 
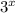, получим уравнение 
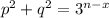. Поскольку числа p и q не делятся на 3, а величина n-x больше 0, это уравнение корней не имеет. Наконец, рассмотрим случай, когда x≠y, в силу симметрии можно считать, что x<y. Разделив уравнение на 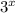, имеем 
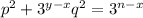. Первое слагаемое не делится на 3, второе и третье делятся, получили противоречие.
было сначала преп --- 10
замена 1 на 3
всего замен --- 12
всего преп ?
Решение.
При замене препятствие, которое не удалось обойти, заменяется другим, так, что начальное число необходимых сохраняется, но при каждой замене появляется два новых, штрафных препятствия, которые надо преодолеть. И Антон это все сделал! Он и необходимое число, и все дополнительные штрафные, возникающие по ходу игры.
3 - 1 = 2 (п.) настолько увеличивается число препятствий при каждой замене
2 * 12 = 24 (п.) всего было пройдено дополнительных препятствий
10 + 24 = 34 (п.) всего пройдено препятствий
ответ: 34 препятствия
все
x=2
Пошаговое объяснение:
1.раскрыть скобки
78x+624-50=730
2.вычеслить
78x+574=730
3.перенести константу в правую часть равенства
78x=730-574
4.вычеслить
78x=156
5.разделить обе стороны
х=2