Ряд сходится, но не сходится абсолютно
Пошаговое объяснение:
Домножим каждый член ряда на 3, от этого сходимость не поменяется, так что с этого места считаем, что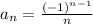 
.
Заметим, что ряд составленный из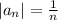 
является гармоническим рядом, который, как известно, расходится. Поэтому ряд не сходится абсолютно. Чтобы доказать просто сходимость, разобьем слагаемые попарно:
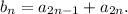
Заметим, что
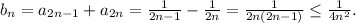Заметим, что ряд составленный из 
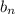сходится, так как он составлен из положительных членов и мажорируется сходящимся рядом 
Обозначим частичные суммы ряда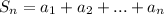 
.
Тогда в наших обозначения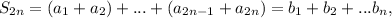 
а ряд из 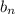сходится, значит 
имеет предел. Обозначим этот предел за 
. Для окончания доказательства, докажем что частичные суммы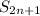 
тоже сходятся к a.
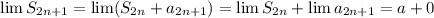, так как очевидно, что 
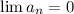. Итого, мы доказали, что у частичных сумм есть предел , значит ряд сходится по определению
Пошаговое объяснение:
1) задание
Дано
Прямоугольный параллелепипед
a=8 дм
b=5 дм
h=7дм
Sпол.=?
Решение
Sпол.=2ab+2bh+2ah
Sпол.=2*8*5+2*7*8+2*7*5=80+112+70=
=262 см²
ответ: площадь полной поверхности параллелепипеда 262 см²
2)
Дано
Треугольная призма
a=5 cm сторона треугольника
b=8 cm сторона треугольника
c=7 cm сторона треугольника
h=3 cm высота
Sбок.=?
Решение
Sбок.=аh+bh+ch
Sбок.=5*3+8*3+7*3=15+24+21=60 см²
ответ: площадь боковой поверхности призмы 60см²
3)
Дано
Правильная четырехугольная призма
Основание квадрат
а=60 см сторона квадрата
h=20 cm высота.
Sпол.=2Sосн.+4Sгр.
Sосн.=а²
Sгр.=аh
Sпол.=2*60²+4*60*20=7200+4800=
=12000 cm²
ответ: площадь полной поверхности призмы 12000 см²