а) Плоскость альфа параллельна AB, M принадлежит альфа, P принадлежит альфа .
Через точку P в плоскости (ABB_1) проведём PQ параллельна AB . Тогда плоскость (PQM) искомая по признаку параллельности прямой и плоскости (PQ параллельна AB , следовательно, (PQM) параллельна AB).
1 случай. Точка M совпадает с точкой A. В этом случае плоскость (PQM) (т. е. альфа) совпадает с (ABB_1) , сечение — прямоугольник (ABB_1 A_1) , и с учётом равенства трёх сторон получаем квадрат со стороной, равной 16 и периметром 64, что больше 40.
2 случай. Точка M находится внутри отрезка AC. В этом случае плоскость (PQM) не совпадает с (ABB_1) . Построим сечение призмы плоскостью (PQM). Пусть плоскость (PQM) пересекает нижнюю грань по прямой MN, N принадледит BC , тогда MN параллельна AB , ( в противном случае MN пересекается с AB в некоторой точке T и мы получаем противоречие: через три точки P, Q и T проходят две различные плоскости). Соединяя точки P и N, получаем искомое сечение PQMN.
Так как ABPQ — параллелограмм (AQ параллельна BP, AВ параллельна PQ) , даже прямоугольник, то AB = PQ = 16.
б) Решение по построению
Ответ: 24корень из 3 разделить на корень из 91
"Как я воспитана" Я получила хорошее воспитание в своей интелигентной семье. Мои родители уделяют большое внимание моему воспитанию. Они стараются вырастить из меня образованного интелегентного человека. Моя мама ежедневно занимается со мной уроками музыки, учит меня готовить, проверяет моë домашнее задание, мы вместе с ней занимаемся йогой, она покупает мне интересные книги, которые я с удовольствием читаю. Мой папа занимается со мной сортом: зимой мы по выходным ездим на горнолыжную трассу и проводим там целый день, а летом мы месте с ним каждый вечер ездим на велосипеде. Они многое мне дают
-10
Пошаговое объяснение:
Нам тут понадобится правило Лопиталя.
если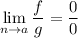 или
или 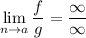 то
то 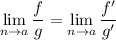
1
2 Вынесем -1 по формуле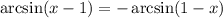
3 Запишем предел произведения дробей как произведение пределов
4 Подставим в первом пределе значение и посчитаем
5 Cоберем квадрат в знаменателе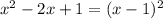
6 Получили предел вида воспользуемся правилом Лопиталя
воспользуемся правилом Лопиталя
Тут я сразу вынес за скобки
7 Вынесем (взял 2 в знаменателе) за предел и сократим
(взял 2 в знаменателе) за предел и сократим
8 Распишем как произведение пределов
9 Посчитаем первый предел
10 Распишем разность дробей в пределе
11 Распишем предел разности как разность пределов
12 Распишем первый предел как произведение пределов и вынесем 5π
13 Посчитаем первый предел
14 В первом пределе снова неопределённость , снова Лопиталем
, снова Лопиталем
15 Теперь мы можем посчитать первый предел
16 Снова используем правило Лопиталя, так как у нас неопределённость
17 Выносим константу
18 Посчитаем предел
19 Досчитываем!
МЫ ПОЛУЧИЛИ ОТВЕТ