Математика: 4 3/5 x + x + 2 1/2 x + 7 / 15 x + 3 1/10х , если х = 9/14,1 4/5 ,решение

Можно найти несколько пределов данной числовой последовательности. Для этого нужно посмотреть, что произойдет с ней при стремлении к бесконечности с разными знаками, и в опасных точках. Опасные точки сразу видны, это: 1) - знаменатель обращается в 0. 2) - по обычаю проверяется эта точка. Эта числовая последовательность может быть сведена ко второму замечательному пределу для нахождения пределов: (при →∞) Выделяем целую часть в дроби: Используем свойство 2-го замечательного предела, но добавляем...

4 3/5 x + x + 2 1/2 x + 7 / 15 x + 3 1/10х , если х = 9/14,1 4/5 ,решение

👇

Увидеть ответ

Ответ:

xeniaverner

30.10.2020

Пошаговое объяснение:

= (4 3/5 + 1 + 2 1/2 + 7/15 + 3 1/10)x = (17 + 18/30 + 15/30 + 14/30 + 3/30)x = 17 + 1 + 2/3)x = 18 2/3 x = 56/3 x

При x = 9/14

56/3 · 9/14 = 12

При x = 1 4/5 = 9/5

56/3 · 9/5 = 33 3/5

4,6(75 оценок)

Открыть все ответы

Ответ:

София9354

30.10.2020

В прямоугольном параллелепипеде все грани - прямоугольники, все рёбра равны и перпендикулярны основаниям.

Формула диагонали квадрата d=a√2 ⇒

Диагональ АС основания равна 4√2

Из прямоугольного треугольника АА1С по т.Пифагора боковое ребро

АА1=√(А1С²-AC²)=√(81-32)=7 (ед. длины)

-------

Вариант решения.

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Измерениями прямоугольного параллелепипеда являются длины трех ребер, исходящих из одной его вершины. Отсюда следует:

D²=a²+b²+c², где а и b- стороны основания, с - боковое ребро.

По условию а=b=4. D=9

81=16+16+c² ⇒

c²=81-32=49

c=7 - длина бокового ребра.

Основанием прямоугольного параллепипеда служит квадрат со стороной, равной 4. диагональ параллепипед

4,8(97 оценок)

Ответ:

LoveSmile78900987

30.10.2020

Можно найти несколько пределов данной числовой последовательности. Для этого нужно посмотреть, что произойдет с ней при стремлении к бесконечности с разными знаками, и в "опасных" точках.

"Опасные" точки сразу видны, это:
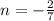1) $n=- \frac{2}{7}$ - знаменатель обращается в 0.
2) n=0

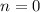- по обычаю проверяется эта точка.

Эта числовая последовательность может быть сведена ко второму замечательному пределу для нахождения пределов:
$lim (1+ \frac{1}{x})^x=e$ (при

→∞)

Выделяем целую часть в дроби:

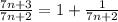
$\frac{7n+3}{7n+2 } = 1 + \frac{1}{7n+2 }$

Используем свойство 2-го замечательного предела, но добавляем степени:

$lim (1 + \frac{1}{7n+2 })^{3n-4}$

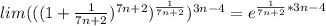$lim (((1 + \frac{1}{7n+2 })^{7n+2})^{ \frac{1}{7n+2}})^{3n-4} = e^{\frac{1}{7n+2} * 3n-4}$ (при

→∞)

То есть мы степень не меняли: домножили и разделили.

Посчитаем, что получилось:

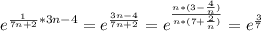$e^{\frac{1}{7n+2} * 3n-4} = e^{ \frac{3n-4}{7n+2}} = e^{ \frac{n*(3-\frac{4}{n}) }{n*(7+\frac{2}{n})} } = e^{ \frac{3}{7} }$ (при

→∞)

Итак:
1)

→+∞ предел равен $e^{ \frac{3}{7} }$
2)

→-∞ предел равен $e^{ \frac{3}{7} }$

3)

→0 предел равен:
$lim ( \frac{7n+3}{7n+2})^{3n-4} = (\frac{3}{2})^{-4} = (\frac{2}{3})^{4} = \frac{16}{81}$

4)

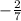
→ $- \frac{2}{7}$
По правило Лопиталя имеем: 0 (не расписывал, поскольку это очень много и неважно в данном случае, нас это не интересует).

Мы видим, что при стремлении к бесконечности с разными знаками, мы имеем конечное число. В "опасных" точках, скачков нет.

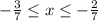Используя свойства показательной функции, находим, что график делает скачок в некотором интервале (основание должно быть неотрицательным числом, если же взять число из интервала $- \frac{3}{7} \leq x \leq - \frac{2}{7}$ - мы получаем отрицательное основание).

Можно говорить, что данная числовая последовательность является неограниченной (из-за этого интервала).

Если же этого не учитывать, то данная числовая последовательность является ограниченной (это очень грубо).

Найдите предел числовой последовательности. укажите, является ли заданная числовая последовательност